
分析 (1)任取a,b∈[-1,1],且a<b,则b-a>0,结合(x+y)[f(x)+f(y)]>0,判断出f(b)>-f(-a),结合函数单调性的定义,可得结论;
(2)若f(x+$\frac{1}{2}$)<f(1-2x),则-1≤x+$\frac{1}{2}$<1-2x≤1,解得原不等式的解集;
(3)f(x)max=f(1)=1,故m2-2m-2≥1,解得实数m的范围.
解答 解:(1)f(x)是定义在[-1,1]上的增函数,理由如下:
任取a,b∈[-1,1],且a<b,则b-a>0,
∵(x+y)[f(x)+f(y)]>0,
∴(b-a)[f(b)+f(-a)]>0,
即f(b)+f(-a)>0,
即f(b)>-f(-a),
∵函数是定义在[-1,1]上的奇函数,
∴f(b)>f(a),
∴f(x)是定义在[-1,1]上的增函数,
(2)∵f(x+$\frac{1}{2}$)<f(1-2x),
-1≤x+$\frac{1}{2}$<1-2x≤1
解得:x∈[0,$\frac{1}{6}$)
(3)∵f(x)在[-1,1]上单调递增,
所以f(x)max=f(1)=1,
即:对任意的x在[-1,1]上有m2-2m-2≥1成立,
解得:m≥3或m≤-1
点评 本题考查的知识点是抽象函数的应用,函数的奇偶性与函数的单调性,函数恒成立问题,难度中档.


科目:高中数学 来源: 题型:解答题
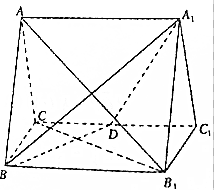 如图,正三棱柱ABC-A1B1C1的所有棱长都有2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都有2,D为CC1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
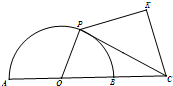 如图,已知半圆O的半径为1,点C在直径AB的延长线上,且BC=1,P是半圆上动点,以PC为一边作等腰直角三角形PCK(K为直角顶点,且K和O在PC的两侧).
如图,已知半圆O的半径为1,点C在直径AB的延长线上,且BC=1,P是半圆上动点,以PC为一边作等腰直角三角形PCK(K为直角顶点,且K和O在PC的两侧).查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com