在等差数列{an}中,前四项之和为60,最后四项之和为100,所有项之和是120,则项数n为( )
A.3
B.4
C.5
D.6
【答案】
分析:将已知条件中的四项相加,利用等差数列的性质求出a
1+a
n,再利用等差数列的前n项和公式列出有关n的等式求出n的值.
解答:解:∵a
1+a
2+a
3+a
4=60
a
n+a
n-1+a
n-2+a
n-3=100
两式相加得
4(a
1+a
n)=160
∴a
1+a
n=40
∵
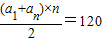
即
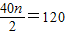
解得n=6
故选D
点评:解决等差数列的项的和问题与解决等比数列的项的积问题,一般利用它们的性质.等差数列中有:若m+n=p+q则有a
m+a
n=a
p+a
q;对于等比数列有若m+n=p+q则有a
m•a
n=a
p•a
q
