
| A. | (-$\frac{17}{8}$,-2) | B. | (-$\frac{17}{8}$,-2] | C. | [1,$\frac{17}{16}$) | D. | (1,$\frac{17}{16}$) |
分析 求得x>0的图象关于原点对称的图象的解析式.由题意可得方程2-x2=-3|x+a|+a在x<0时有三个不等的实根.通过去绝对值,讨论a的正负,解出二次方程的根,判断正负,结合判别式大于0,解不等式即可得到所求a的范围.
解答 解:当x>0时,f(x)=x2-2关于原点对称的图象对应的函数解析式为y=-x2+2(x<0),
由题意可得方程2-x2=-3|x+a|+a在x<0时有三个不等的实根.
若a≤0时,方程即为x2+3x+4a-2=0最多有2个不等实根,故不成立;
当a>0时,若x≥-a时,方程即为x2-3x-2a-2=0,
解得x=$\frac{3±\sqrt{17+8a}}{2}$,舍去正的,可得x=$\frac{3-\sqrt{17+8a}}{2}$;
若x<-a,方程即为x2+3x+4a-2=0,由题意可得判别式大于0,
即为9-4(4a-2)>0,解得a<$\frac{17}{16}$.解得x=$\frac{-3±\sqrt{17-16a}}{2}$.
由$\frac{3-\sqrt{17+8a}}{2}$≥-a,$\frac{-3-\sqrt{17-16a}}{2}$<-a,且$\frac{-3+\sqrt{17-16a}}{2}$<-a,
可得a≥1且0<a<<$\frac{17}{16}$且1<a<<$\frac{17}{16}$.
即有a的范围是(1,$\frac{17}{16}$).
故选:D.
点评 本题考查函数的图象关于原点对称问题的解法,注意运用转化思想,绝对值的意义,讨论二次方程的根的分布情况,考查化简整理的运算能力,属于中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
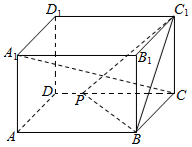 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.| A. | 1+2π | B. | 1+$\frac{4π}{3}$ | C. | 1+$\frac{π}{2}$ | D. | 1+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{a}$<x<1} | B. | {x|-1<x<$\frac{1}{a}$} | C. | {x|1$<x<\frac{1}{a}$} | D. | {x|-$\frac{1}{a}$<x<-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com