【题目】已知双曲线
(a>b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 ( )
A. 
B. 
C. 2 D. 
【答案】D
【解析】
连接
，利用题设条件和双曲线的定义分别求得求得
，再在
和
中，利用余弦定理求得
和
，又由
，即可化简得到答案.
连接F1Q,设F1(-c,0),F2(c,0),则|PF1|=|F1F2|=2c.
由双曲线的定义可得|PF2|=|PF1|-2a=2c-2a,
∴由3|PF2|=2|QF2|,可得|QF2|=3c-3a,
∴由双曲线的定义可得|QF1|=|QF2|+2a=3c-a.
在△PF1F2和△QF1F2中,cos∠F1F2P=
=
=
,
cos∠F1F2Q=
=
=
.
由∠F1F2Q+∠F1F2P=π,可得cos∠F1F2Q+cos∠F1F2P=0,
即有+=0,化简得5c=7a,所以e==.
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且满足向量 
=（cosA，cosB）， 
=（a，2c﹣b）， ∥ ．
（1）求角A的大小；
（2）若a=2 
，求△ABC面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，椭圆C： 
=1（a＞1）的左、右顶点分别为A、B，P是椭圆C上任一点，且点P位于第一象限．直线PA交y轴于点Q，直线PB交y轴于点R．当点Q坐标为（0，1）时，点R坐标为（0，2）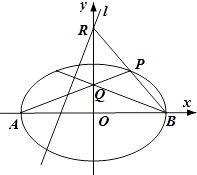 
（1）求椭圆C的标准方程；
（2）求证： 
为定值；
（3）求证：过点R且与直线QB垂直的直线经过定点，并求出该定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi（单位:千元）与月储蓄yi（单位:千元）的数据资料,算得
＝80, 
＝20, 
＝184, 
＝720．
（Ⅰ）求家庭的月储蓄y对月收入x的线性回归方程y＝bx＋a;
（Ⅱ）判断变量x与y之间是正相关还是负相关;
（Ⅲ）若该居民区某家庭月收入为7千元,预测该家庭的月储蓄．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则AP与平面PDE所成角的正弦值为 ( )
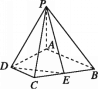
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，圆C1：（x﹣1）2+y2=2，圆C2：（x﹣m）2+（y+m）2=m2 ． 圆C2上存在点P满足：过点P向圆C1作两条切线PA，PB，切点为A，B，△ABP的面积为1，则正数m的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一个特定时段内，以点
为中心的
海里以内海域被设为警戒水域．点正北50海里处有一个雷达观测站
．某时刻测得一艘匀速直线行驶的船只位于点北偏东
且与点相距
海里的位置
，经过
分钟又测得该船已行驶到点北偏东
且与点
相距
海里的位置
．
（1）求该船的行驶速度（单位：海里/小时）；
（2）若该船不改变航行方向继续行驶，判断它是否会进入警戒水域，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
