练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某高校调查了200名学生每周的自习时间(单位：小时)，制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)，[20，22.5)，[22.5，25)，[25，27.5)，[27.5，30]．根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是

    A. 56 B. 60 C. 120 D. 140

    【答案】D

    【解析】

    根据已知中的频率分布直方图，先计算出自习时间不少于22.5小时的频率，进而可得自习时间不少于22.5小时的频数．

    根据频率分布直方图，200名学生中每周的自习时间不少于22.5小时的频率为(0.16＋0.08＋0.04)×2.5＝0.7，

    故200名学生中每周的自习时间不少于22.5小时的人数为200×0.7＝140.

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，平面ABCD⊥平面ADEF，其中四边形ABCD为矩形，四边形ADEF为梯形，AF∥DE，AF⊥EF，AF＝AD＝2AB＝2DE＝2．

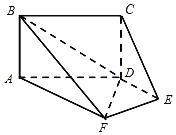
    （1）求证：CE∥面ABF；

    （2）求直线DE与平面BDF所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的函数存在零点，且对任意都满足，若关于的方程（）恰有三个不同的根，则实数的取值范围是____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标坐标系中，曲线的参数方程为（为参数），曲线： .以为极点， 轴的非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系.

    （1）求曲线的极坐标方程；

    （2）射线（）与曲线的异于极点的交点为，与曲线的交点为，求.

    【答案】(1) 的极坐标方程为， 的极坐标方程为；(2) .

    【解析】试题分析：（1）先根据三角函数平方关系消参数得曲线，再根据将曲线的极坐标方程；（2）将代人曲线的极坐标方程，再根据求.

    试题解析：（1）曲线的参数方程（为参数）

    可化为普通方程，

    由，可得曲线的极坐标方程为，

    曲线的极坐标方程为.

    （2）射线（）与曲线的交点的极径为，

    射线（）与曲线的交点的极径满足，解得，

    所以.

    【题型】解答题
    【结束】
    23

    【题目】设函数．

    （1）设的解集为，求集合；

    （2）已知为（1）中集合中的最大整数，且（其中，，为正实数），求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若关于的方程恰有两个不相等的实数根， 则实数的取值范围是

    A. B. ， C. ， D. ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ，其中．函数的图象过点，点与其相邻的最高点的距离为4．

    （Ⅰ）求函数的单调递减区间；

    （Ⅱ）计算的值；

    （Ⅲ）设函数，试讨论函数在区间 [0，3] 上的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在△中， ， 分别为， 的中点， 为的中点， ， ．将△沿折起到△的位置，使得平面平面， 为的中点，如图2．

    （1）求证： 平面；

    （2）求证：平面平面；

    （3）线段上是否存在点，使得平面？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有下列命题：①若，则；②若，则存在唯一实数，使得；③若，则；④若，且与的夹角为钝角，则；⑤若平面内定点满足，则为正三角形.其中正确的命题序号为 ________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）在同一半周期内的图象过点， ， ，其中为坐标原点， 为函数图象的最高点， 为函数的图象与轴的正半轴的交点， 为等腰直角三角形.

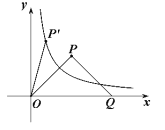
    （1）求的值；

    （2）将绕原点按逆时针方向旋转角，得到，若点恰好落在曲线（）上（如图所示），试判断点是否也落在曲线（）上，并说明理由.

    查看答案和解析>>

    同步练习册答案