
ĄūĖâÄŋĄŋČįÍžĢŽÔÚąūĘÐÄģūÉÐĄĮøļÄÔėđĪģĖÖÐĢŽÐčŌŠÔÚĩØÏÂÆĖÉčĖėČžÆøđÜĩĀ.ŌŅÖŠÐĄĮøÄģīĶČýīą·ŋÎÝ·ÖąðÎŧÓÚÉČÐÎ![]() ĩÄČýļöķĨĩãÉÏĢŽĩã
ĩÄČýļöķĨĩãÉÏĢŽĩã![]() ĘĮŧĄ
ĘĮŧĄ![]() ĩÄÖÐĩãĢŽÏÖÓûÔÚÏßķÎ
ĩÄÖÐĩãĢŽÏÖÓûÔÚÏßķÎ![]() ÉÏÕŌŌŧīĶŋŠÍÚđĪŨũŋÓ
ÉÏÕŌŌŧīĶŋŠÍÚđĪŨũŋÓ![]() ĢĻēŧÓëĩã
ĢĻēŧÓëĩã![]() ĢŽ
ĢŽ![]() ÖØšÏĢĐĢŽÎŠÆĖÉčČýĖõĩØÏÂĖėČžÆøđÜÏß
ÖØšÏĢĐĢŽÎŠÆĖÉčČýĖõĩØÏÂĖėČžÆøđÜÏß![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽŌŅÖŠ
ĢŽŌŅÖŠ![]() ÃŨĢŽ
ÃŨĢŽ![]() ĢŽžĮ
ĢŽžĮ![]() ĢŽļÃČýĖõĩØÏÂĖėČžÆøđÜÏßĩÄŨÜģĪķČΊ
ĢŽļÃČýĖõĩØÏÂĖėČžÆøđÜÏßĩÄŨÜģĪķČΊ![]() ÃŨ.
ÃŨ.

ĢĻ1ĢĐ―Ŧ![]() ąíĘūģÉ
ąíĘūģÉ![]() ĩÄšŊĘýĢŽēĒÐīģö
ĩÄšŊĘýĢŽēĒÐīģö![]() ĩÄ·ķΧĢŧ
ĩÄ·ķΧĢŧ
ĢĻ2ĢĐĮëČ·ķĻđĪŨũŋÓ![]() ĩÄÎŧÖÃĢŽĘđīËīĶĩØÏÂĖėČžÆøđÜÏßĩÄŨÜģĪķČŨîÐĄĢŽēĒĮóģöŨÜģĪķČĩÄŨîÐĄÖĩ.
ĩÄÎŧÖÃĢŽĘđīËīĶĩØÏÂĖėČžÆøđÜÏßĩÄŨÜģĪķČŨîÐĄĢŽēĒĮóģöŨÜģĪķČĩÄŨîÐĄÖĩ.
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ĢŧĢĻ2ĢĐĩą
ĢŧĢĻ2ĢĐĩą![]() ģĪΊ
ģĪΊ![]() ÃŨĘąĢŽīËīĶĖėČžÆøđÜÏßĩÄģĪķČŨîķĖΊ
ÃŨĘąĢŽīËīĶĖėČžÆøđÜÏßĩÄģĪķČŨîķĖΊ![]() ÃŨ.
ÃŨ.
Ąū―âÎöĄŋ
ĢĻ1ĢĐĀûÓÃÕýÏŌķĻĀíŋÉĮóĩÃ![]() ĄĒ
ĄĒ![]() ĢŽīÓķøĩÃĩ―
ĢŽīÓķøĩÃĩ―![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() .
.
ĢĻ2ĢĐĀûÓÃĩžĘýŋÉĮó![]() ĩÄŨîÐĄÖĩ.
ĩÄŨîÐĄÖĩ.
ĢĻ1ĢĐŌōΊ![]() ΊŧĄ
ΊŧĄ![]() ĩÄÖÐĩãĢŽÓÉķÔģÆÐÔŋÉÖŠĢŽ
ĩÄÖÐĩãĢŽÓÉķÔģÆÐÔŋÉÖŠĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ÓÖ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ÓÉÕýÏŌķĻĀíĢŽĩÃ![]() ĢŽ
ĢŽ
ÓÖ![]() ĢŽĩÃ
ĢŽĩÃ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ËųŌÔ![]()
![]() ĢŽ
ĢŽ
ÓÉĖâŌâĢŽ![]() ĩÄČĄÖĩ·ķΧĘĮ
ĩÄČĄÖĩ·ķΧĘĮ![]() .
.
ĢĻ2ĢĐÁî![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
Ôō![]() ĢŽÁî
ĢŽÁî![]() ĢŽĩÃ
ĢŽĩÃ![]() ĢŽ
ĢŽ
ÁÐąíĢš
|
|
|
|
|
|
| - | 0 | + | ||
|
| žŦÐĄÖĩ |
|
ËųŌÔĩą![]() ĘąĢŽ
ĘąĢŽ![]() ÃŨĢŽ
ÃŨĢŽ![]() ÓÐÎĻŌŧžŦÐĄÖĩ
ÓÐÎĻŌŧžŦÐĄÖĩ![]() .
.
īËĘą![]() ÓÐŨîÐĄÖĩ
ÓÐŨîÐĄÖĩ![]() ÃŨ.
ÃŨ.
īðĢšĩą![]() ģĪΊ
ģĪΊ![]() ÃŨĘąĢŽīËīĶĖėČžÆøđÜÏßĩÄģĪķČŨîķĖΊ
ÃŨĘąĢŽīËīĶĖėČžÆøđÜÏßĩÄģĪķČŨîķĖΊ![]() ÃŨ.
ÃŨ.



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
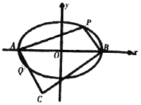
ĄūĖâÄŋĄŋŌŅÖŠÔēūßÓÐŌÔÏÂÐÔÖĘĢšÉčAĢŽBĘĮÔēCĢš![]() ÉÏđØÓÚÔĩãķÔģÆĩÄÁ―ĩãĢŽĩãPĘĮÔēÉÏĩÄČÎŌâŌŧĩãĢŪČôÖąÏßPAĢŽPBĩÄÐąÂĘķžīæÔÚēĒ·ÖąðžĮΊ
ÉÏđØÓÚÔĩãķÔģÆĩÄÁ―ĩãĢŽĩãPĘĮÔēÉÏĩÄČÎŌâŌŧĩãĢŪČôÖąÏßPAĢŽPBĩÄÐąÂĘķžīæÔÚēĒ·ÖąðžĮΊ![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() Ģ―Đ1ĢŽĘĮÓëĩãPĩÄÎŧÖÃÎÞđØĩÄķĻÖĩĢŪ
Ģ―Đ1ĢŽĘĮÓëĩãPĩÄÎŧÖÃÎÞđØĩÄķĻÖĩĢŪ
ĢĻ1ĢĐĘÔĀāąČÔēĩÄÉÏĘöÐÔÖĘĢŽÐīģöÍÖÔē![]() ĩÄŌŧļöĀāËÆÐÔÖĘĢŽēĒžÓŌÔÖĪÃũĢŧ
ĩÄŌŧļöĀāËÆÐÔÖĘĢŽēĒžÓŌÔÖĪÃũĢŧ
ĢĻ2ĢĐČįÍžĢŽČôÍÖÔēMĩÄąęŨž·―ģĖΊ![]() ĢŽĩãPÔÚÍÖÔēMÉÏĮŌÎŧÓÚĩÚŌŧÏóÏÞĢŽĩãAĢŽB·ÖąðΊÍÖÔēģĪÖáĩÄÁ―ļöķËĩãĢŽđýĩãAĢŽB·ÖąðŨũ
ĢŽĩãPÔÚÍÖÔēMÉÏĮŌÎŧÓÚĩÚŌŧÏóÏÞĢŽĩãAĢŽB·ÖąðΊÍÖÔēģĪÖáĩÄÁ―ļöķËĩãĢŽđýĩãAĢŽB·ÖąðŨũ![]() ĄÍPAĢŽ
ĄÍPAĢŽ![]() ĄÍPBĢŽÖąÏß
ĄÍPBĢŽÖąÏß![]() ĢŽ
ĢŽ![]() ―ŧÓÚĩãCĢŽÖąÏß
―ŧÓÚĩãCĢŽÖąÏß![]() ÓëÍÖÔēMĩÄÁíŌŧ―ŧĩãΊQĢŽĮŌ
ÓëÍÖÔēMĩÄÁíŌŧ―ŧĩãΊQĢŽĮŌ![]() ĢŽĮó
ĢŽĮó![]() ĩÄČĄÖĩ·ķΧĢĻŋÉÖą―ÓĘđÓÃĢĻ1ĢĐÖÐÖĪÃũĩÄ―áÂÛĢĐĢŪ
ĩÄČĄÖĩ·ķΧĢĻŋÉÖą―ÓĘđÓÃĢĻ1ĢĐÖÐÖĪÃũĩÄ―áÂÛĢĐĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģŌ―ŌĐŋŠ·ĒđŦËūĘĩŅéĘŌÓÐ![]() ÆŋČÜŌšĢŽÆäÖÐ
ÆŋČÜŌšĢŽÆäÖÐ![]() ÆŋÖÐÓÐÏļūú
ÆŋÖÐÓÐÏļūú![]() ĢŽÏÖÐčŌŠ°ŅšŽÓÐÏļūú
ĢŽÏÖÐčŌŠ°ŅšŽÓÐÏļūú![]() ĩÄČÜŌšžėŅéģöĀīĢŽÓÐČįÏÂÁ―ÖÖ·―°ļĢš
ĩÄČÜŌšžėŅéģöĀīĢŽÓÐČįÏÂÁ―ÖÖ·―°ļĢš
·―°ļŌŧĢšÖðÆŋžėŅéĢŽÔōÐčžėŅé![]() īÎĢŧ
īÎĢŧ
·―°ļķþĢšŧėšÏžėŅéĢŽ―Ŧ![]() ÆŋČÜŌš·ÖąðČĄŅųĢŽŧėšÏÔÚŌŧÆðžėŅéĢŽČôžėŅé―áđûēŧšŽÓÐÏļūú
ÆŋČÜŌš·ÖąðČĄŅųĢŽŧėšÏÔÚŌŧÆðžėŅéĢŽČôžėŅé―áđûēŧšŽÓÐÏļūú![]() ĢŽÔō
ĢŽÔō![]() ÆŋČÜŌšČŦēŋēŧšŽÓÐÏļūú
ÆŋČÜŌšČŦēŋēŧšŽÓÐÏļūú![]() ĢŧČôžėŅé―áđûšŽÓÐÏļūú
ĢŧČôžėŅé―áđûšŽÓÐÏļūú![]() ĢŽūÍŌŠķÔÕâ
ĢŽūÍŌŠķÔÕâ![]() ÆŋČÜŌšÔŲÖðÆŋžėŅéĢŽīËĘąžėŅéīÎĘýŨÜđēΊ
ÆŋČÜŌšÔŲÖðÆŋžėŅéĢŽīËĘąžėŅéīÎĘýŨÜđēΊ![]() .
.
(1)žŲÉč![]() ĢŽēÉÓ÷―°ļŌŧĢŽĮóĮĄšÃžėŅé3īÎūÍÄÜČ·ķĻÄÄÁ―ÆŋČÜŌššŽÓÐÏļūú
ĢŽēÉÓ÷―°ļŌŧĢŽĮóĮĄšÃžėŅé3īÎūÍÄÜČ·ķĻÄÄÁ―ÆŋČÜŌššŽÓÐÏļūú![]() ĩÄļÅÂĘĢŧ
ĩÄļÅÂĘĢŧ
(2)ÏÖķÔ![]() ÆŋČÜŌš―øÐОėŅéĢŽŌŅÖŠÃŋÆŋČÜŌššŽÓÐÏļūú
ÆŋČÜŌš―øÐОėŅéĢŽŌŅÖŠÃŋÆŋČÜŌššŽÓÐÏļūú![]() ĩÄļÅÂĘūųΊ
ĩÄļÅÂĘūųΊ![]() .
.
ČôēÉÓ÷―°ļŌŧ.ÐčžėŅéĩÄŨÜīÎĘýΊ![]() ,ČôēÉÓ÷―°ļķþ.ÐčžėŅéĩÄŨÜīÎĘýΊ
,ČôēÉÓ÷―°ļķþ.ÐčžėŅéĩÄŨÜīÎĘýΊ![]() .
.
(i)Čô![]() Óë
Óë![]() ĩÄÆÚÍûÏāĩČ.ĘÔĮó
ĩÄÆÚÍûÏāĩČ.ĘÔĮó![]() đØÓÚ
đØÓÚ![]() ĩÄšŊĘý―âÎöĘ―
ĩÄšŊĘý―âÎöĘ―![]() ;
;
(ii)Čô![]() ,ĮŌēÉÓ÷―°ļķþŨÜīÎĘýĩÄÆÚÍûÐĄÓÚēÉÓ÷―°ļŌŧŨÜīÎĘýĩÄÆÚÍû.Įó
,ĮŌēÉÓ÷―°ļķþŨÜīÎĘýĩÄÆÚÍûÐĄÓÚēÉÓ÷―°ļŌŧŨÜīÎĘýĩÄÆÚÍû.Įó![]() ĩÄŨîīóÖĩ.
ĩÄŨîīóÖĩ.
ēÎŋžĘýūÝĢš![]()
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() ĢŽ
ĢŽ
(1)·ÖąðĮó![]() ĩÄÖĩ:
ĩÄÖĩ:
(2)ĖÖÂÛ![]() ĩÄ―âĩÄļöĘý:
ĩÄ―âĩÄļöĘý:
(3)ČôķÔČÎŌâļøķĻĩÄ![]() ,ķžīæÔÚÎĻŌŧĩÄ
,ķžīæÔÚÎĻŌŧĩÄ![]() ,ÂúŨã
,ÂúŨã![]() ĢŽĮóĘĩĘý
ĢŽĮóĘĩĘý![]()
ĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋΊÁËĩũēéÄģīóŅ§Ņ§ÉúÔÚÄģĖėÉÏÍøĩÄĘąžäĢŽËæŧúķÔ100ÃûÄÐÉúšÍ100ÃûÅŪÉú―øÐÐÁËēŧžĮÃûĩÄÎĘūíĩũēéĢŽĩÃĩ―ÁËČįÏÂĩÄÍģžÆ―áđûĢš

(1)ČôļÃīóŅ§đēÓÐÅŪÉú750ČËĢŽĘÔđĀžÆÆäÖÐÉÏÍøĘąžäēŧÉŲÓÚ60·ÖÖÓĩÄČËĘýĢŧ
(2)ÍęģÉÁŠąíĢŽēĒŧØīðÄÜ·ņÓÐ90%ĩÄ°ŅÎÕČÏΊĄ°īóŅ§ÉúÉÏÍøĘąžäÓëÐÔąðÓÐđØĄą.

ļ―Ģš![]() ĢŽÆäÖÐnĢ―aĢŦbĢŦcĢŦdΊŅųąūČÝÁŋ.
ĢŽÆäÖÐnĢ―aĢŦbĢŦcĢŦdΊŅųąūČÝÁŋ.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘýf(x)Ģ―x(lnxĢax)ÓÐÁ―ļöžŦÖĩĩãĢŽÔōĘĩĘýaĩÄČĄÖĩ·ķΧĘĮ(ĄĄĄĄ )
A. (ĢĄÞĢŽ0) B. ![]() C. (0,1) D. (0ĢŽĢŦĄÞ)
C. (0,1) D. (0ĢŽĢŦĄÞ)
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÍÖÔē![]() ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊ
ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊ![]() ĢŽđýÔĩã
ĢŽđýÔĩã![]() ĮŌÐąÂĘΊ1ĩÄÖąÏß
ĮŌÐąÂĘΊ1ĩÄÖąÏß![]() ―ŧÍÖÔē
―ŧÍÖÔē![]() ÓÚ
ÓÚ![]() Á―ĩãĢŽËÄąßÐÎ
Á―ĩãĢŽËÄąßÐÎ![]() ĩÄÖÜģĪÓëÃæŧý·ÖąðΊ8Óë
ĩÄÖÜģĪÓëÃæŧý·ÖąðΊ8Óë![]() .
.
(Ēņ)ĮóÍÖÔē![]() ĩÄąęŨž·―ģĖĢŧ
ĩÄąęŨž·―ģĖĢŧ
(Ēō)ÉčÖąÏß![]() ―ŧÍÖÔē
―ŧÍÖÔē![]() ÓÚ
ÓÚ![]() Á―ĩãĢŽĮŌ
Á―ĩãĢŽĮŌ![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() ĩ―ÖąÏß
ĩ―ÖąÏß![]() ĩÄūāĀëΊķĻÖĩ.
ĩÄūāĀëΊķĻÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋËÄĀâĖĻąŧđýĩã![]() ĩÄÆ―Ãæ―ØČĨŌŧēŋ·ÖšóĩÃĩ―ČįÍžËųĘūĩÄžļšÎĖåĢŽÆäÏÂĩŨÃæËÄąßÐÎ
ĩÄÆ―Ãæ―ØČĨŌŧēŋ·ÖšóĩÃĩ―ČįÍžËųĘūĩÄžļšÎĖåĢŽÆäÏÂĩŨÃæËÄąßÐÎ![]() ĘĮąßģĪΊ2ĩÄÁâÐÎĢŽ
ĘĮąßģĪΊ2ĩÄÁâÐÎĢŽ![]() ĢŽ
ĢŽ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽ
ĢŽ![]() .
.
ĢĻĒņĢĐĮóÖĪĢšÆ―Ãæ![]() Æ―Ãæ
Æ―Ãæ![]() Ģŧ
Ģŧ
ĢĻĒōĢĐČô![]() ÓëĩŨÃæ
ÓëĩŨÃæ![]() ËųģÉ―ĮĩÄÕýĮÐÖĩΊ2ĢŽĮóķþÃæ―Į
ËųģÉ―ĮĩÄÕýĮÐÖĩΊ2ĢŽĮóķþÃæ―Į![]() ĩÄÓāÏŌÖĩ.
ĩÄÓāÏŌÖĩ.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽ![]() ĘĮÔēOĩÄÖąūķĢŽĩãCĘĮÔēOÉÏŌėÓÚAĢŽBĩÄĩãĢŽÖąÏß
ĘĮÔēOĩÄÖąūķĢŽĩãCĘĮÔēOÉÏŌėÓÚAĢŽBĩÄĩãĢŽÖąÏß![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽEĢŽF·ÖąðĘĮ
ĢŽEĢŽF·ÖąðĘĮ![]() ĢŽ
ĢŽ![]() ĩÄÖÐĩã.
ĩÄÖÐĩã.

ĢĻ1ĢĐžĮÆ―Ãæ![]() ÓëÆ―Ãæ
ÓëÆ―Ãæ![]() ĩÄ―ŧÏßΊlĢŽĘÔÅÐķÏÖąÏßlÓëÆ―Ãæ
ĩÄ―ŧÏßΊlĢŽĘÔÅÐķÏÖąÏßlÓëÆ―Ãæ![]() ĩÄÎŧÖÃđØÏĩĢŽēĒžÓŌÔÖĪÃũĢŧ
ĩÄÎŧÖÃđØÏĩĢŽēĒžÓŌÔÖĪÃũĢŧ
ĢĻ2ĢĐÉč![]() ĢŽĮóķþÃæ―Į
ĢŽĮóķþÃæ―Į![]() īóÐĄĩÄČĄÖĩ·ķΧ.
īóÐĄĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com