
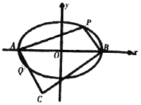
����Ŀ����֪Բ�����������ʣ���A��B��ԲC��![]() �Ϲ���ԭ��ԳƵ����㣬��P��Բ�ϵ�����һ�㣮��ֱ��PA��PB��б�ʶ����ڲ��ֱ��Ϊ
�Ϲ���ԭ��ԳƵ����㣬��P��Բ�ϵ�����һ�㣮��ֱ��PA��PB��б�ʶ����ڲ��ֱ��Ϊ![]() ��
��![]() ����
����![]() ����1�������P��λ���صĶ�ֵ��
����1�������P��λ���صĶ�ֵ��
��1�������Բ���������ʣ�д����Բ![]() ��һ���������ʣ�������֤����
��һ���������ʣ�������֤����
��2����ͼ������ԲM�ı�����Ϊ![]() ����P����ԲM����λ�ڵ�һ���ޣ���A��B�ֱ�Ϊ��Բ����������˵㣬����A��B�ֱ���
����P����ԲM����λ�ڵ�һ���ޣ���A��B�ֱ�Ϊ��Բ����������˵㣬����A��B�ֱ���![]() ��PA��
��PA��![]() ��PB��ֱ��
��PB��ֱ��![]() ��
��![]() ���ڵ�C��ֱ��
���ڵ�C��ֱ��![]() ����ԲM����һ����ΪQ����
����ԲM����һ����ΪQ����![]() ����
����![]() ��ȡֵ��Χ����ֱ��ʹ�ã�1����֤���Ľ��ۣ���
��ȡֵ��Χ����ֱ��ʹ�ã�1����֤���Ľ��ۣ���
���𰸡���1����֤������2��![]()
��������
��1�����![]() �����
�����![]() ����
����![]() ������Բ���̴��뻯��ɵý⣻
������Բ���̴��뻯��ɵý⣻
��2����AP��б��Ϊk��![]() ����ϣ�1���еĽ��ۿɵ�ֱ��AC��BC��BQ�ķ��̣�����ֱ�߷��̿ɵ�
����ϣ�1���еĽ��ۿɵ�ֱ��AC��BC��BQ�ķ��̣�����ֱ�߷��̿ɵ�![]() ��
��![]() ����
����![]() �����
�����![]() �ɵý�.
�ɵý�.
��1�����ʣ���A��B����Բ![]() �Ϲ���ԭ��ԳƵ����㣬��
�Ϲ���ԭ��ԳƵ����㣬��![]() ����Բ�ϵ�����һ�㣮��ֱ��
����Բ�ϵ�����һ�㣮��ֱ��![]() ��
��![]() ��б�ʶ����ڲ��ֱ��Ϊ
��б�ʶ����ڲ��ֱ��Ϊ![]() ��
��![]() ����
����![]() �����
�����![]() ��λ���صĶ�ֵ��
��λ���صĶ�ֵ��
֤�������![]() �����
�����![]() ���Ӷ�
���Ӷ�![]() �����
�����![]() ��
��![]() ��
��
�� ��
��
��![]() �����P��λ���صĶ�ֵ��
�����P��λ���صĶ�ֵ��
��2����AP��б��Ϊk��![]() ����ΪPΪ��ԲM�ϵ�һ������һ�㣬����
����ΪPΪ��ԲM�ϵ�һ������һ�㣬����![]() �ɣ�1�����ۿ�֪
�ɣ�1�����ۿ�֪![]() ������BP��б��Ϊ
������BP��б��Ϊ![]() ��
��
��Ϊ![]() ������
������![]() ����AC�ķ���Ϊ
����AC�ķ���Ϊ![]()
��Ϊ![]() ������
������![]() ����BC�ķ���Ϊ
����BC�ķ���Ϊ![]() .
.
�� ����
����![]() ����
����![]()
��![]() ����Ϊ
����Ϊ![]() ��
��
��ֱ��![]() ��б��
���![]() ������
������![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() �ķ���Ϊ
�ķ���Ϊ![]()
�������� ����
����![]() ����
����![]()
��
��Ϊ![]() ������
������![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ�ijҽԺ�������ȡ����λҽ����Ա�Ĺذ����߿��˷��������߿��ˣ�10���ƣ�������ص�������![]() ��ʾ��ҽ��רҵ֪ʶ���˷������Ծ����ԣ�100���ƣ�������ص�������
��ʾ��ҽ��רҵ֪ʶ���˷������Ծ����ԣ�100���ƣ�������ص�������![]() ��ʾ���������±���
��ʾ���������±���
������![]() ����
����![]() �����Իع鷽�̣���������ȷ��0.01����
�����Իع鷽�̣���������ȷ��0.01����
�������ã�I���е����Իع鷽�̣�����ҽ��רҵ���˷����ı仯�Թذ����߿��˷�����Ӱ�죬������ijҽ����Ա��ҽ��רҵ֪ʶ���˷���Ϊ95��ʱ�����Ĺذ����߿��˷�������ȷ��0.1����

������Ҫ��ҽ��רҵ֪ʶ���˷���95�����µ�ҽ����Ա��ѡ��2�˲μ��齨�ġ���կ���ֺ�ҽ��С�ֶӡ���ѵ������������������һ�˿��˷�����90�����µĸ���.
�����ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�
��֪����![]() ��aΪʵ����.
��aΪʵ����.
��1����![]() ʱ������
ʱ������![]() ��ͼ����
��ͼ����![]() �������߷��̣�
�������߷��̣�
��2����![]() ������
������![]() �ϵ���Сֵ��
�ϵ���Сֵ��
��3����������������ʵ��![]() ��ʹ����
��ʹ����![]() ��������ʵ��a��ȡֵ��Χ.
��������ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����˾ӵ������100��.��ÿ�����������Ϊ![]() Ԫʱ����ȫ�����.��ÿ�����������ÿ����50Ԫʱ��δ����ij���������һ��.����ij�ÿ��ÿ����Ҫά����150Ԫ��δ����ij�ÿ��ÿ����Ҫά����50Ԫ.��ʹ����˾�����������ÿ�����������Ӧ�ö�Ϊ__________��
Ԫʱ����ȫ�����.��ÿ�����������ÿ����50Ԫʱ��δ����ij���������һ��.����ij�ÿ��ÿ����Ҫά����150Ԫ��δ����ij�ÿ��ÿ����Ҫά����50Ԫ.��ʹ����˾�����������ÿ�����������Ӧ�ö�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���Բ![]() ��
�� ![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ����Բ
����Բ![]() �ϣ�
�ϣ�
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����֪![]() ��
��![]() Ϊƽ���ڵ��������㣬��
Ϊƽ���ڵ��������㣬��![]() ���ֱ��
���ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
�� ![]() ���㣬���ı���
���㣬���ı���![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǹ����ִ�������Ҫָ�꣬���й�������ʾ��1978��2013�꣬�ҹ�����ס�˿ڴ�1.7�����ӵ�7.3�ڣ�����ÿһ�����ס�˿ڵ�����������ȣ���1978����t����![]() ����ij���ס�˿�Ϊ
����ij���ס�˿�Ϊ![]() �ڣ�д��
�ڣ�д��![]() �Ľ���ʽ�����ɴ˹�����ҹ�2017��ij���ס�˿�����
�Ľ���ʽ�����ɴ˹�����ҹ�2017��ij���ס�˿�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ���ⳤΪ
���ⳤΪ![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣬���
���е㣬���![]() ����
����![]() ƽ�е�ƽ������������ý�������Ϊ____________
ƽ�е�ƽ������������ý�������Ϊ____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ���ij��С�����칤���У���Ҫ�ڵ���������ȼ���ܵ�.��֪С��ij���������ݷֱ�λ������![]() �����������ϣ���
�����������ϣ���![]() �ǻ�
�ǻ�![]() ���е㣬�������߶�
���е㣬�������߶�![]() ����һ�����ڹ�����
����һ�����ڹ�����![]() �������
�������![]() ��
��![]() �غϣ���Ϊ��������������ȼ������
�غϣ���Ϊ��������������ȼ������![]() ��
��![]() ��
��![]() ����֪
����֪![]() �ף�
�ף�![]() ����
����![]() ��������������ȼ�����ߵ��ܳ���Ϊ
��������������ȼ�����ߵ��ܳ���Ϊ![]() ��.
��.

��1����![]() ��ʾ��
��ʾ��![]() �ĺ�������д��
�ĺ�������д��![]() �ķ�Χ��
�ķ�Χ��
��2����ȷ��������![]() ��λ�ã�ʹ�˴�������ȼ�����ߵ��ܳ�����С��������ܳ��ȵ���Сֵ.
��λ�ã�ʹ�˴�������ȼ�����ߵ��ܳ�����С��������ܳ��ȵ���Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com