
(本小题满分12分)数列 中,已知
中,已知 ,
, 时,
时, .数列
.数列 满足:
满足: .
.
(Ⅰ)证明: 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对 ;若不存在,说明理由.
;若不存在,说明理由.
(Ⅰ)详见解析,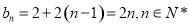 ;(Ⅱ)
;(Ⅱ)  .
.
【解析】
试题分析:(Ⅰ)本题的落脚点在 上,所以首先从条件
上,所以首先从条件 的特征入手,里面有因式
的特征入手,里面有因式 ,提示我们可以考虑在条件
,提示我们可以考虑在条件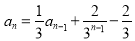 中构造
中构造 ,从而使条件特征显现出来,成为解题的突破口;(Ⅱ)充分利用(Ⅰ)中的结论并结合已知求出
,从而使条件特征显现出来,成为解题的突破口;(Ⅱ)充分利用(Ⅰ)中的结论并结合已知求出 的通项,从而求得
的通项,从而求得 ,将之代入题设中的不等式,通过一系列推理、化简、变形即可得出所求,变形过程应特别注意不等号两边的结构相似性.
,将之代入题设中的不等式,通过一系列推理、化简、变形即可得出所求,变形过程应特别注意不等号两边的结构相似性.
试题解析:(Ⅰ)当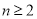 时,
时,
由 ,
,
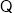
 ,即
,即 时,
时,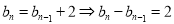 ,又
,又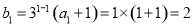 ,
,
 数列
数列 是首项为2,公差为2的等差数列,
是首项为2,公差为2的等差数列,
由等差数列的通项公式得: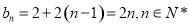 ;
;
(Ⅱ)由(Ⅰ)得, ,所以
,所以 ,
,
则 ,
,
由 ,得
,得 ,
,
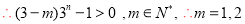
当 时,
时, ;当
;当 时,
时,
综上,存在符合条件的所有有序实数对 为:
为: .
.
考点:①根据递推公式,构造性求解数列通项;②等差数列的定义和通项公式;③等比数列的前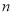 项和公式;④不等式的基本性质;⑤变形、运算、比较的能力和技巧.
项和公式;④不等式的基本性质;⑤变形、运算、比较的能力和技巧.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
将三个分别标有A,B,C的球随机放入编号为1,2,3,4的四个盒子中,则1号盒子中有球的不同放法种数为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:填空题
已知在平面直角坐标系下,点 分别为
分别为 轴和
轴和 轴上的两个动点,满足
轴上的两个动点,满足 ,点
,点 为线段
为线段 的中点,已知点
的中点,已知点 ,
, ,则
,则 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:选择题
给定正整数 按下图方式构成三角形数表;第一行依次写上数
按下图方式构成三角形数表;第一行依次写上数 ,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依次类推,最后一行(第
,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比下一行少一个数),依次类推,最后一行(第 行)只有一个数.例如
行)只有一个数.例如 时数表如图所示,则当
时数表如图所示,则当 时最后一行的数是
时最后一行的数是

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:填空题
执行如图所示的程序框图,若输入如下四个函数:
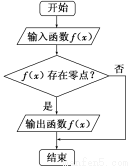
①y=2x;②y=-2x; ③f(x)=x+x-1;④f(x)=x-x-1.
则输出函数的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com