
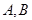 是椭圆
是椭圆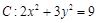 上两点,点M的坐标为
上两点,点M的坐标为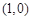 .
.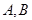 两点关于
两点关于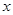 轴对称,且
轴对称,且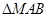 为等边三角形时,求
为等边三角形时,求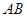 的长;
的长;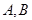 两点不关于
两点不关于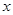 轴对称时,证明:
轴对称时,证明: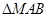 不可能为等边三角形.
不可能为等边三角形. 或
或 ,(2)详见解析.
,(2)详见解析.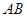 的长,实际求出
的长,实际求出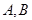 坐标.利用正三角形性质列等量关系.设
坐标.利用正三角形性质列等量关系.设 ,
, ,则
,则 .又点
.又点 在椭圆上,所以
在椭圆上,所以 解得
解得 或
或 ,
, 或
或 ,(2)本题实际应用逆否命题与原命题等价进行解题,即当
,(2)本题实际应用逆否命题与原命题等价进行解题,即当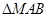 为等边三角形时,
为等边三角形时,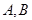 两点必关于
两点必关于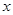 轴对称,即横坐标相等.设
轴对称,即横坐标相等.设 ,则由
,则由 ,可化简
,可化简 ,同理可得
,同理可得 ,而
,而 ,因此
,因此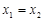 或
或 又
又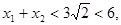 所以
所以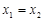 .
. ,
, , 1分
, 1分 为等边三角形,所以
为等边三角形,所以 . 2分
. 2分 在椭圆上,
在椭圆上, 消去
消去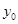 , 3分
, 3分 ,解得
,解得 或
或 , 4分
, 4分 时,
时, ;
; 时,
时, . 5分
. 5分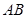 斜率存在.
斜率存在.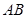 :
: ,
, ,
, ,
,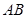 中点为
中点为 ,
, 消去
消去 得
得 , 6分
, 6分 得到
得到 ① 7分
① 7分 ,
, , 8分
, 8分 ,又
,又
 为等边三角形,则有
为等边三角形,则有 , 9分
, 9分 ,即
,即 , 10分
, 10分 ,② 11分
,② 11分 ,代入①得
,代入①得 ,
,  ,不成立, 13分
,不成立, 13分 或
或 或
或 都给分}
都给分} 不能为等边三角形. -14分
不能为等边三角形. -14分 ,则
,则 ,且
,且 ,
, , 8分
, 8分 ,同理可得
,同理可得 ,且
,且 9分
9分 在
在 上单调
上单调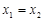

 , 11分
, 11分 不关于
不关于 轴对称,所以
轴对称,所以 .
. , -13分
, -13分 不可能为等边三角形. 14分
不可能为等边三角形. 14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com