
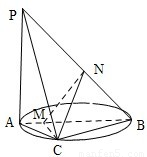
 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,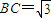 ,
,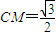 ,
,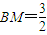 .
.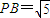 .
.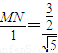 .
. .
.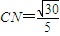 .故cos
.故cos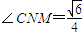 .
. .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
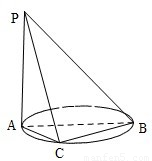
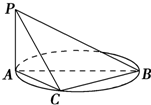 如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:
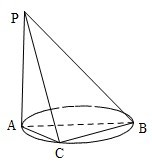 (2013•辽宁)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(2013•辽宁)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.查看答案和解析>>
科目:高中数学 来源:2013-2014学年吉林长春十一中高二上学期期初考试理科数学试卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.
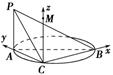
(1)求证:平面PAC⊥平面PBC;(6分)
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(6分)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.
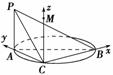
(1)求证:平面PAC⊥平面PBC;(6分)
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(6分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com