练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙两人玩猜数字游戏，规则如下：
    ①连续竞猜3次，每次相互独立；
    ②每次竞猜时，先由甲写出一个数字，记为a，再由乙猜甲写的数字，记为b，已知a，b∈{0,1,2,3,4,5}，若|a－b|≤1，则本次竞猜成功；
    ③在3次竞猜中，至少有2次竞猜成功，则两人获奖．
    求甲乙两人玩此游戏获奖的概率．

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛．若每盘比赛中高一、高二获胜的概率分别为，.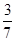
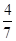    (1)按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？
    (2)若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130 t该农产品．以X(单位： t,100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．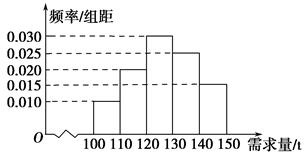

    (1)将T表示为X的函数；
    (2)根据直方图估计利润T不少于57 000元的概率；
    (3)在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若x∈[100,110)，则取X＝105，且X＝105的概率等于需求量落入[100,110)的频率，求T的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A配方和B配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
    A配方的频数分布表

    指标值分组
    		[90,94)
    		[94,98)
    		[98,102)
    		[102,106)
    		[106,110)
    频数
    		8
    		20
    		42
    		22
    		8
    B配方的频数分布表
    指标值分组
    		[90,94)
    		[94,98)
    		[98,102)
    		[102,106)
    		[106,110)
    频数
    		4
    		12
    		42
    		32
    		10
    (1)分别估计用A配方，B配方生产的产品的优质品率；
    (2)已知用B配方生产的一件产品的利润y(单位：元)与其质量指标值t的关系式为y＝从用B配方生产的产品中任取一件，其利润记为X(单位：元)，求X的分布列及数学期望．(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校为组建校篮球队，对报名同学进行定点投篮测试，规定每位同学最多投3次，每次在A或B处投篮，在A处投进一球得3分，在B处投进一球得2分，否则得0分，每次投篮结果相互独立，将得分逐次累加并用X表示，如果X的值不低于3分就认为通过测试，立即停止投篮，否则继续投篮，直到投完三次为止．投篮方案有以下两种：
    方案1：先在A处投一球，以后都在B处投；
    方案2：都在B处投篮．
    已知甲同学在A处投篮的命中率为0.4，在B处投篮的命中率为0.6.
    (1)甲同学若选择方案1，求X＝2时的概率；
    (2)甲同学若选择方案2，求X的分布列和数学期望；
    (3)甲同学选择哪种方案通过测试的可能性更大？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下列表：

     
    		喜爱打篮球
    		不喜爱打篮球
    		合计
    男生
    		 
    		5
    		 
    女生
    		10
    		 
    		 
    合计
    		 
    		 
    		50
    已知在全部50人中随机抽取1人，抽到喜爱打篮球的学生的概率为．
    （1）请将上表补充完整(不用写计算过程)；
    （2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理
    由；下面的临界值表供参考：

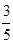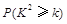    		0.15
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

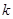    		2.072
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
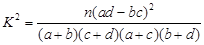    (参考公式：，其中)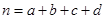

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    本着健康、低碳的生活理念，租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费，超过两小时的部分每小时收费标准为2元（不足1小时的部分按1小时计算）。有甲乙两人相互独立来该租车点租车骑游（各租一车一次），设甲、乙不超过两小时还车的概率分别为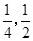；两小时以上且不超过三小时还车的概率分别为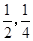；两人租车时间都不会超过四小时.
    （1）求出甲、乙两人所付租车费用相同的概率；
    （2）设甲、乙两人所付的租车费用之和为随机变量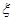，求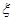的分布列与数学期望.

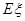    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某工厂甲、乙两个车间包装同一种产品，在自动包装传送带上每隔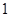小时抽一包产品，称其重量（单位：克）是否合格，分别记录抽查数据，获得重量数据的茎叶图如图所示.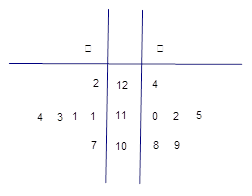

    （1）根据样品数据，计算甲、乙两个车间产品重量的平均值与方差，并说明哪个车间的产品的重量相对较稳定；
    （2）若从乙车间件样品中随机抽取两件，求所抽取的两件样品的重量之差不超过克的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
    (1)若随机数b,c∈{1,2,3,4}.
    (2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b="4*Rand(" )和c="4*Rand(" )的执行结果.(注:符号“*”表示“乘号”)

    查看答案和解析>>

    同步练习册答案