|
|
|
已知函数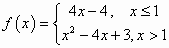 与g(x)=log2x则函数h(x)=f(x)-g(x)的零点个数是________. 与g(x)=log2x则函数h(x)=f(x)-g(x)的零点个数是________.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
关于x的不等式: 的解集为[m,n],若n-m=3,则实数k的值等于________. 的解集为[m,n],若n-m=3,则实数k的值等于________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据:
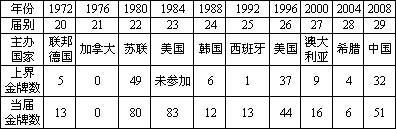
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,求出主办国在上届所获金牌数(设为x)与在当届所获金牌数(设为y)之间的线性回归方程 = = ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数) ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数)
|
| [ ] |
A. |
29块
|
B. |
30块
|
C. |
31块
|
D. |
32块
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设Sn是等差数列{an}的前n项和,若 = =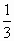 ,则 ,则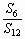 等于 等于
|
| [ ] |
A. |
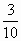
|
B. |
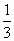
|
C. |
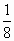
|
D. |
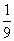
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
定义在R的函数y=ln(x2+1)+|x|,满足f(2x-1)>f(x+1),则x满足的关系是
|
| [ ] |
A. |
(2,+∞)∪(-∞,-1)
|
B. |
(2,+∞)∪(-∞,1)
|
C. |
(-∞,1)∪(3,+∞)
|
D. |
(2,+∞)∪(-∞,-1)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=x2-alnx(常数a>0).
(Ⅰ)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)讨论函数f(x)在区间(1,ea)上零点的个数(e为自然对数的底数).
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知等差数列{an}的前n项和为Sn,若a4=18-a5则S8等于
|
| [ ] |
A. |
18
|
B. |
36
|
C. |
54
|
D. |
72
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数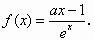
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若对任意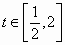 ,f(t)>t恒成立,求实数a的取值范围. ,f(t)>t恒成立,求实数a的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若规定一种对应关系f(k),使其满足:
①f(k)=(m,n)(m<n),且n-m=k;
②如果f(k)=(m,n),那么f(k+1)=(n,r)(m,n,r∈N*).
若已知f(1)=(2,3),则
(1)f(2)=________;
(2)f(n)=________.
|
|
|
查看答案和解析>>
