
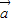 与
与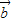 的夹角为60°,
的夹角为60°,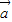 =(2,0),|
=(2,0),|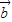 |=1,则|
|=1,则|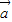 +2
+2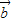 |=( )
|=( )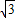
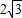
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 6 |
| a |
| 3 |
| b |
| a |
| b |
| AB |
| a |
| b |
| AD |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省外语外贸大学附设外语学校高三(上)数学寒假作业3(文科)(解析版) 题型:选择题
 ,
, ,
, .有下列三个命题:
.有下列三个命题: •
• =
= •
• ,则
,则 =
= .
. =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省六安市寿县一中高三(上)第四次月考数学试卷(理科)(解析版) 题型:填空题
 ,
, ,
, .有下列命题:
.有下列命题: =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥b,则k=-3; ②若|
∥b,则k=-3; ②若| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°;
的夹角为60°; +
+ |=|
|=| |+|
|+| |?
|? 与
与 的方向相同; ④|
的方向相同; ④| |+|
|+| |>|
|>| -
- |?
|? 与
与 的夹角为锐角;
的夹角为锐角; =(1,-3),
=(1,-3), =(-2,4),
=(-2,4), =(4,-6),则表示向量4
=(4,-6),则表示向量4 ,3
,3 -2
-2 ,
, 的有向线段首尾连接能构成三角形.
的有向线段首尾连接能构成三角形.查看答案和解析>>
科目:高中数学 来源:《2.1-2.2 平面向量的概念及其线性运算》2011年同步练习(解析版) 题型:填空题
 ,
, ,
, ,有下列三个命题:
,有下列三个命题: •
• =
= •
• ,则
,则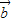 =
= 、
、 =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥
∥ ,则k=-3.
,则k=-3. 和
和 满足|
满足| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°.
的夹角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com