
分析 根据题意,画出图形,结合图形,得出D是BC的中点,且$\frac{|\overrightarrow{AO}|}{|\overrightarrow{OD}|}$=4;从而求出△OAB与△OBC的面积比.
解答 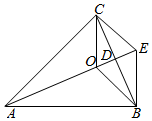 解:根据题意,画出图形,如图所示;
解:根据题意,画出图形,如图所示;
∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+2$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴2($\overrightarrow{OB}$+$\overrightarrow{OC}$)=-$\overrightarrow{OA}$=$\overrightarrow{AO}$,
∴D是BC的中点,且$\frac{|\overrightarrow{AO}|}{|\overrightarrow{OD}|}$=$\frac{4}{1}$;
∴$\frac{{S}_{△OBC}}{{S}_{△ABC}}$=$\frac{1}{5}$,
∴$\frac{{S}_{△OBC}}{{S}_{△OAB}}$=$\frac{1}{(5-1)×\frac{1}{2}}$=$\frac{1}{2}$,
所以△OAB与△OBC的面积比为2:1
故答案额:2:1.
点评 本题考查了平面向量的应用问题,解题时应画出图形,结合图形解答问题,是基础题目.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
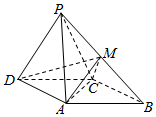 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,平面PDC⊥平面ABCD,AC=AD=PD=PC,∠DAC=90°,M在PB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,围建一个面积为100m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为56元/米,新墙的造价为200元/米,设利用的旧墙长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元)
如图,围建一个面积为100m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为56元/米,新墙的造价为200元/米,设利用的旧墙长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com