考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则
P(A)=,P(B)=,P()=,P()=,进而根据“甲、乙两人各投球一次,都命中”的事件为A∩B,代入相互独立事件概率乘法公式,得到答案;
(2)事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,利用对立事件概率减法公式,可得答案.
解答:
解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
则
P(A)=,P(B)=,P()=,P()=.
∵“甲、乙两人各投球一次,都命中”的事件为A∩B,且是相互独立的,
∴
P(A∩B)=P(A)•P(B)=×=.
答:甲、乙两人在罚球线各投球一次,都命中的概率为
.
(2)∵事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,
事件“甲、乙两人在罚球线各投球一次均不命中”的概率为
=×=,
∴甲、乙两人在罚球线各投球一次至少有一次命中的概率
P=1-=1-=.
点评:本题考查的知识点是互斥事件的概率加法公式,对立事件的概率减法公式,分析事件之间的关系是解答的关键.



 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案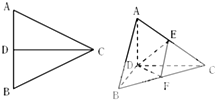 已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.