Question

【题目】某通信公司为了配合客户的不同需要，现设计A，B两种优惠方案，这两种方案的应付话费y（元）与通话时间x(分钟)之间的关系如图所示(实线部分)．(注：图中MN∥CD)

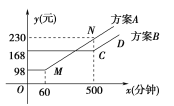
（1）若通话时间为2小时，则按方案A，B各付话费多少元？

（2）方案B从500分钟以后，每分钟收费多少元？

（3）通话时间在什么范围内，方案B才会比方案A优惠？

Answer 1

【答案】（1）分别为116元，168元；（2）0.3元；（3）通话时间在时，方案B才会比方案A优惠.

【解析】

根据函数图象写出函数解析式，（1）代入求值；（2）根据计算即可；（3）分别比较当0≤x≤60时，当x>500时，当60<x<时，当≤x≤500时，的大小即可.

由图可知M(60，98)，N(500，230)，C(500，168)，MN∥CD.

设这两种方案的应付话费与通话时间的函数关系分别为fA（x），fB（x），

则fA（x）＝,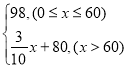

fB（x）＝.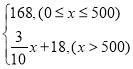

（1）通话2小时，, ,

两种方案的话费分别为116元，168元．

（2）因为fB(n＋1)－fB（n）＝ (n＋1)＋18－n－18＝0.3，(n>500)，

所以方案B从500分钟以后，每分钟收费0.3元．

（3）由图可知，当0≤x≤60时，有fA（x）<fB（x）．

当x>500时，fA（x）>fB（x）．

当60<x≤500时，168＝x＋80，解得x＝.

当60<x<时，fB（x）>fA（x）；

当≤x≤500时，fA（x）>fB（x）．

即当通话时间在时，方案B才会比方案A优惠．