
如图,已知正三棱柱 的各棱长都是4,
的各棱长都是4, 是
是 的中点,动点
的中点,动点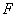 在线段
在线段 上,且不与点
上,且不与点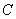 、
、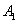 重合.
重合.
(1)若 ,求平面
,求平面 与平面
与平面 的夹角的余值;
的夹角的余值;
(2)求点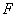 到直线
到直线 距离
距离 的最小值.
的最小值.

科目:高中数学 来源: 题型:
设函数f(x)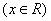 满足f(
满足f(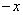 )=f(x),f(x)=f(2
)=f(x),f(x)=f(2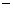 x),且当
x),且当 时,f(x)=x3.又函数g(x)=|xcos
时,f(x)=x3.又函数g(x)=|xcos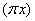 |,则函数h(x)=g(x)-f(x)在
|,则函数h(x)=g(x)-f(x)在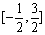 上的零点个数为
上的零点个数为
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S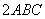 =S△BCM·S△BCD.上述命题是( )
=S△BCM·S△BCD.上述命题是( )
A.真命题
B.增加条件“AB⊥AC”才是真命题
C.增加条件“M为△BCD的垂心”才是真命题
D.增加条件“三棱锥A-BCD是正三棱锥”才是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy 中,曲线C1的参数方程为 (
( 为参数)
为参数)
M是C1上的动点,P点满足 ,P点的轨迹为曲线C2.
,P点的轨迹为曲线C2.
(1)求C2的方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
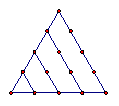 在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形
在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形
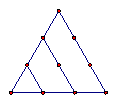
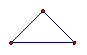
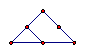

1 3 6 10 15
则第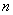 个三角形数为( )
个三角形数为( )
A.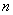 B
B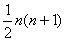 C.
C.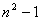 D.
D.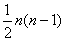
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com