
分析 根据抛物线的对称性可知,若正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,则另外两个定点关于x轴对称,就可的直线OA的倾斜角,据此求出直线OA的方程,与抛物线方程联立解出A点坐标,就可求出正三角形的边长.
解答  解:∵抛物线y2=2px关于x轴对称,
解:∵抛物线y2=2px关于x轴对称,
∴若正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,
则A,B点关于x轴对称,
∴直线OA倾斜角为30°,斜率为$\frac{\sqrt{3}}{3}$
∴直线OA方程为y=$\frac{\sqrt{3}}{3}$x,
代入抛物线方程,可得A(6p,2$\sqrt{3}$p),则B(6p,-2$\sqrt{3}$p),
∴|AB|=4$\sqrt{3}$p
∴这个正三角形的边长为4$\sqrt{3}$p
故答案为:4$\sqrt{3}$p.
点评 本题主要考查了抛物线的对称性,直线方程的点斜式,以及曲线交点的求法,属于圆锥曲线的综合题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
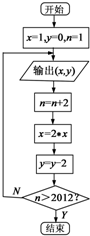 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com