
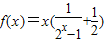 ,
,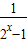 +
+ )=
)=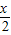 •
•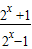 ,
,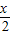 •
•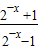 =
=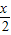 •
•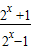 =f(x),
=f(x),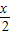 •
•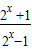 ,
,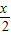 •
•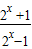 >0;
>0;

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源:2011-2012学年湖北省武汉市部分重点中学(五校)高一(上)期中数学试卷(解析版) 题型:解答题
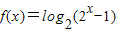 ,
,查看答案和解析>>
科目:高中数学 来源:2009-2010学年贵州省黔西南州兴仁县百德中学高三(上)10月月考数学试卷(解析版) 题型:解答题
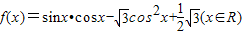 ,
,查看答案和解析>>
科目:高中数学 来源:2012年新疆乌鲁木齐高级中学高考数学押题试卷(文科)(解析版) 题型:解答题
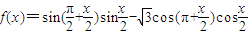 .
.查看答案和解析>>
科目:高中数学 来源:3年高考2年模拟:4.2 三角函数的图象和性质及三角恒等变换(6)(解析版) 题型:解答题
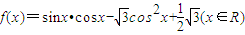 ,
,查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三9月月考试卷理科数学 题型:解答题
(本小题满分12分) 已知函数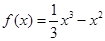 .
.
(1)求f (x)的极值;
(2) 已知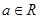 ,设函数
,设函数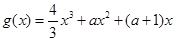 的单调递减区间为
的单调递减区间为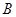 ,且
,且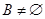 ,
,
函数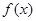 的单调递减区间为
的单调递减区间为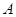 ,若
,若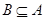 ,求
,求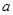 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com