
已知函数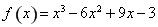 .
.
(1)求函数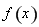 的极值;
的极值;
(2)定义:若函数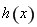 在区间
在区间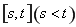 上的取值范围为
上的取值范围为 ,则称区间
,则称区间 为函数
为函数 的“域同区间”.试问函数
的“域同区间”.试问函数 在
在 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
(1)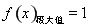 ,
, ;(2)不存在,详见解析.
;(2)不存在,详见解析.
【解析】
试题分析:(1)先求出函数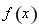 的定义域与导数,求出极值点后,利用图表法确定函数
的定义域与导数,求出极值点后,利用图表法确定函数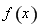 的单调性,从而确定函数
的单调性,从而确定函数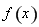 的极大值与极小值;(2)结合(1)中的结论可知,函数
的极大值与极小值;(2)结合(1)中的结论可知,函数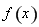 在区间
在区间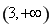 上单调递增,根据定义得到
上单调递增,根据定义得到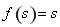 ,
,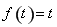 ,问题转化为求方程
,问题转化为求方程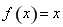 在区间
在区间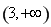 上的实数根,若方程的根的个数小于
上的实数根,若方程的根的个数小于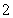 ,则不存在“域同区间”;若上述方程的根的个数不少于
,则不存在“域同区间”;若上述方程的根的个数不少于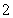 ,则存在“域同区间”,并要求求出相应的根,从而确定相应的“域同区间”.
,则存在“域同区间”,并要求求出相应的根,从而确定相应的“域同区间”.
试题解析:(1)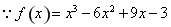 ,定义域为
,定义域为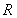 ,
,
且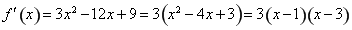 ,
,
令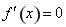 ,解得
,解得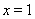 或
或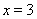 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| 增 | 极大值 | 减 | 极小值 | 增 |
故函数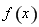 在
在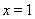 处取得极大值,即
处取得极大值,即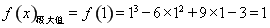 ,
,
函数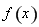 在
在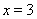 处取得极小值,即
处取得极小值,即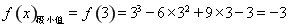 ;
;
(2)由(1)知,函数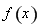 在区间
在区间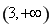 上单调递增,
上单调递增,
假设函数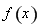 在区间
在区间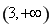 上存在“域同区间”
上存在“域同区间”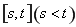 ,则有
,则有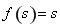 ,
,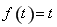 ,
,
则方程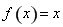 在区间
在区间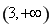 上至少有两个不同的实数根,
上至少有两个不同的实数根,
构造新函数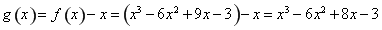 ,定义域为
,定义域为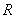 ,
,
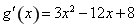 ,令
,令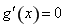 ,解得
,解得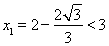 ,
,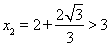 ,
,
当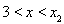 时,
时,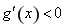 ;当
;当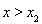 时,
时,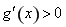 ,
,
故函数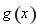 在区间
在区间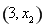 上单调递减,在区间
上单调递减,在区间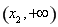 上单调递增,
上单调递增,
因为 ,
,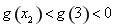 ,
,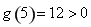 ,故函数
,故函数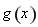 在区间
在区间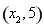 上存在唯一零点,
上存在唯一零点,
即方程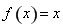 在区间
在区间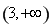 上只存在唯一实数根,
上只存在唯一实数根,
故函数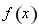 在区间
在区间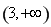 上不存在“域同区间”.
上不存在“域同区间”.
考点:1.函数的极值;2.新定义;3.函数的零点


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取出了ξ个白球,下列概率等于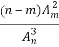 的是( )
的是( )
(A)P(ξ=3) (B)P(ξ≥2)
(C)P(ξ≤3) (D)P(ξ=2)
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
已知A={x|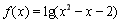 ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|<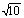 ,i为虚数单位,x>0},则A
,i为虚数单位,x>0},则A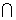 B=( )
B=( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:填空题
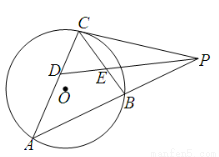
如图,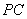 是圆
是圆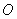 的切线,切点为点
的切线,切点为点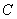 ,直线
,直线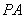 与圆
与圆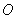 交于
交于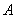 、
、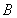 两点,
两点,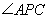 的角平分线交弦
的角平分线交弦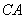 、
、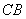 于
于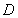 、
、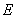 两点,已知
两点,已知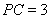 ,
,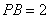 ,则
,则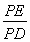 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
一次射击训练,某小组的成绩只有7环、8环、9环三种情况,且该小组的平均成绩为8.15环,设该小组成绩为7环的有x人,成绩为8环、9环的人数情况见下表:
环数(环) | 8 | 9 |
人数(人) | 7 | 8 |
那么x=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:填空题
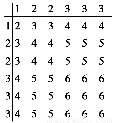
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com