
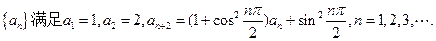
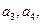 并求数列
并求数列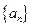 的通项公式;
的通项公式;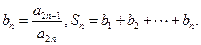 证明:当
证明:当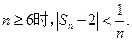
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
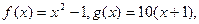 各项均为正数的数列
各项均为正数的数列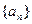 满足
满足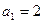 ,
,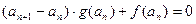 ,
, 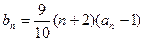 .
.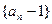 是等比数列;
是等比数列; 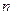 取何值时,
取何值时,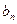 取最大值,并求出最大值;
取最大值,并求出最大值;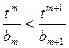 对任意
对任意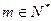 恒成立,求实数
恒成立,求实数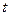 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
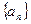 中,
中,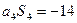 ,
,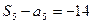 ,其中
,其中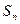 是数列
是数列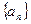 的前
的前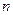 项之和,曲线
项之和,曲线 的方程是
的方程是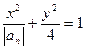 ,直线
,直线 的方程是
的方程是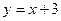 .
.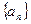 的通项公式;
的通项公式; 与曲线
与曲线 相交于不同的两点
相交于不同的两点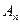 ,
,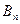 时,令
时,令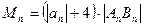 ,
,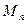 的最小值;
的最小值; 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 为等差数列,
为等差数列, 为其前
为其前 项和
项和
 的反函数为
的反函数为 ,则
,则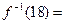 。
。 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。 (
( ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com