
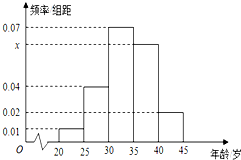
 Ϊ��ǿ����Ľ��ܻ�����ʶ��ij������ȫ��������������־Ը�ߣ��ӷ���������500��־Ը���������ȡ100��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������������ǣ�[20��25����[25��30����[30��35����[35��40����[40��45]��
Ϊ��ǿ����Ľ��ܻ�����ʶ��ij������ȫ��������������־Ը�ߣ��ӷ���������500��־Ը���������ȡ100��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������������ǣ�[20��25����[25��30����[30��35����[35��40����[40��45]������ ��I������С���ε��������Ƶ�ʼ��㼴�ý��ۣ�
��II�����÷ֲ�����ķ�������ѡȡ20������֪X�Ŀ���ȡֵΪ0��1��2��3����������ɵý��ۣ�
��� �⣺��I����С���ε��������Ƶ�ʣ�
���[35��40�����Ƶ�ʺ�Ϊ0.70��
��$x=\frac{1-0.70}{5}=0.06$��
��500��־Ը����������[35��40���������Ϊ0.06��5��500=150���ˣ���
��II���÷ֲ�����ķ���������ѡȡ20����
���������䡰����35�ꡱ������12����
�����䲻����35�ꡱ������8����
��X�Ŀ���ȡֵΪ0��1��2��3��
��$P��{X=0}��=\frac{C_8^3}{{C_{20}^3}}=\frac{14}{285}$��
$P��{X=1}��=\frac{{C_{12}^1C_8^2}}{{C_{20}^3}}=\frac{28}{95}$��
$P��{X=2}��=\frac{{C_{12}^2C_8^1}}{{C_{20}^3}}=\frac{44}{95}$��
$P��{X=3}��=\frac{{C_{12}^3}}{{C_{20}^3}}=\frac{11}{57}$��
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 |
| P | $\frac{14}{285}$ | $\frac{28}{95}$ | $\frac{44}{95}$ | $\frac{11}{57}$ |
���� ���⿼����ɢ�����������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | -4 | C�� | 2 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{2}{7}$ | B�� | $\frac{2}{7}$ | C�� | $-\frac{3}{7}$ | D�� | $\frac{3}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ϲ���˶� | ��ϲ���˶� | �ܼ� | |
| �� | 10 | 18 | |
| Ů | 5 | 12 | |
| �ܼ� | 30 |
| P��x2��x0�� | 0.40 | 0.25 | 0.10 | 0.010 |
| x0 | 0.708 | 1.323 | 2.706 | 6.635 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com