
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 18 | |
| 女 | 5 | 12 | |
| 总计 | 30 |
| P(x2≥x0) | 0.40 | 0.25 | 0.10 | 0.010 |
| x0 | 0.708 | 1.323 | 2.706 | 6.635 |
分析 (1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)假设是否喜爱运动与性别无关,由已知数据可求得观测值,把求得的观测值同临界值进行比较,得到在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关.
(3)喜爱运动的人数为ξ,ξ的取值分别为0,1,2,结合变量对应的事件利用等可能事件的概率公式做出概率,写出分布列和期望.
解答 解:(1)根据条件中所给的a,b,c,d,a+b,a+d,c+d,b+d的值,利用实数的加减运算得到
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 11 | 7 | 18 |
| 女 | 5 | 7 | 12 |
| 总计 | 16 | 14 | 30 |
| ξ | 0 | 1 | 2 |
| P | $\frac{7}{22}$ | $\frac{35}{66}$ | $\frac{5}{33}$ |
点评 本题考查独立性检验的列联表.考查假设性判断,考查离散型随机变量的分布列和期望,是一个综合题.


科目:高中数学 来源: 题型:解答题
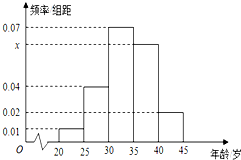 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1+\sqrt{3}i}{2}$ | B. | $\frac{-1-\sqrt{3}i}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com