
| A. | $-\frac{2}{7}$ | B. | $\frac{2}{7}$ | C. | $-\frac{3}{7}$ | D. | $\frac{3}{7}$ |
分析 通过计算出前几项的值可知当n为大于1的奇数时an=$\frac{6}{7}$、当n为大于1的偶数时an=$\frac{3}{7}$,进而计算可得结论.
解答 解:∵${a_1}=\frac{1}{7}$,${a_{n+1}}=\frac{7}{2}{a_n}(1-{a_n})$,
∴a2=$\frac{7}{2}$a1(1-a1)=$\frac{7}{2}$•$\frac{1}{7}$(1-$\frac{1}{7}$)=$\frac{3}{7}$,
a3=$\frac{7}{2}$a2(1-a2)=$\frac{7}{2}$•$\frac{3}{7}$(1-$\frac{3}{7}$)=$\frac{6}{7}$,
a4=$\frac{7}{2}$a3(1-a3)=$\frac{7}{2}$•$\frac{6}{7}$(1-$\frac{6}{7}$)=$\frac{3}{7}$,
∴当n为大于1的奇数时,an=$\frac{6}{7}$,
当n为大于1的偶数时,an=$\frac{3}{7}$,
∴a999-a888=$\frac{6}{7}$-$\frac{3}{7}$=$\frac{3}{7}$,
故选:D.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
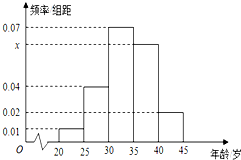 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0.25 | B. | $\frac{1}{2}$log322 | C. | -21log32 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 2 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=$\frac{9}{2}$ | B. | m>$\frac{9}{2}$ | C. | m=9 | D. | m<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com