Question

13．已知函数f（x）=x²-2（a+2）x+a²，g（x）=-x²+2（a-2）x-a²+8．
（1）若f（1）≤8，求实数a的取值范围；
（2）设a=1，对任意的x₁，x₂∈（-1，0），关于m的不等式|$\frac{{x}_{1}}{f（{x}_{1}）}$-g（x₂）|＜m恒成立，求实数m的取值范围；
（3）设H₁（x）=max{f（x，g（x）}，H₂（x）=min{f（x），g（x）}，其中max{p，q}表示p，q中的较大者，min{p，q}表示p，q中的较小者；记H₁（x）的最小值为A，H₂（x）的最大值为B，求A-B的值．

Answer 1

分析 （1）由题意可得a²-2a-11≤0，运用二次不等式的解法可得范围；
（2）分别求得$\frac{x}{f（x）}$，g（x）的范围，由题意可得|$\frac{{x}_{1}}{f（{x}_{1}）}$-g（x₂）|_max＜m，即可得到所求范围；
（3）在同一坐标系中画出f（x）与g（x）的图象，由图象及H₁（x）的定义知H₁（x）的最小值是f（a+2），H₂（x）的最大值为g（a-2），进而可得答案．

解答 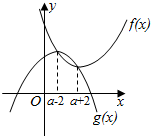解：（1）f（1）≤8，即为a²-2a-11≤0，
解得1-2$\sqrt{3}$≤a≤1+2$\sqrt{3}$；
（2）当a=1时，f（x）=x²-6x+1，g（x）=-x²-2x+7，
即有$\frac{x}{f（x）}$=$\frac{x}{{x}^{2}-6x+1}$=$\frac{1}{x+\frac{1}{x}-6}$，由-1＜x＜0，可得x+$\frac{1}{x}$＜-2，
即有$\frac{x}{f（x）}$∈（-$\frac{1}{8}$，0）；
g（x）=-x²-2x+7=-（x+1）²+8∈（7，8），
由m的不等式|$\frac{{x}_{1}}{f（{x}_{1}）}$-g（x₂）|＜m恒成立，
由|$\frac{{x}_{1}}{f（{x}_{1}）}$-g（x₂）|＜8+$\frac{1}{8}$=$\frac{65}{8}$，
则m≥$\frac{65}{8}$；
（3）令f（x）=g（x），
即x²-2（a+2）x+a²=-x²+2（a-2）x-a²+8，
即x²-2ax+a²-4=0，
解得x=a+2或x=a-2．
f（x）与g（x）的图象如图．
由图象及H₁（x）的定义知H₁（x）的最小值是f（a+2），
H₂（x）的最大值为g（a-2），
则A-B=f（a+2）-g（a-2）
=（a+2）²-2（a+2）²+a²+（a-2）²-2（a-2）²+a²-8=-16．

点评 本题主要考查了二次函数的图象与性质、函数最值的应用等，考查了数形结合的思想，考查运算能力，属于中档题．