
(本小题满分13分)如图,已知抛物线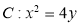 ,过焦点F任作一条直线与
,过焦点F任作一条直线与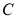 相交于
相交于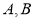 两点,过点
两点,过点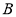 作
作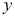 轴的平行线与直线
轴的平行线与直线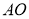 相交于点
相交于点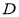 (
(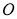 为坐标原点).
为坐标原点).
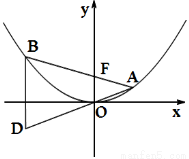
(Ⅰ)证明:动点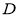 在定直线上;
在定直线上;
(Ⅱ)点P为抛物线C上的动点,直线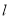 为抛物线C在P点处的切线,求点Q(0,4)到直线
为抛物线C在P点处的切线,求点Q(0,4)到直线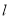 距离的最小值.
距离的最小值.
(Ⅰ)证明见解析(Ⅱ)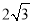
【解析】
试题分析:(1)解决直线和抛物线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式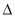 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(2)点Q到直线
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(2)点Q到直线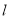 距离的最小值,应先根据题意设出点,再由已知条件求出直线方程,由点到直线的距离公式,可得到一个参数方程,利用基本不等式或函数单调性求出最值即可
距离的最小值,应先根据题意设出点,再由已知条件求出直线方程,由点到直线的距离公式,可得到一个参数方程,利用基本不等式或函数单调性求出最值即可
试题解析:(1)【解析】
依题意,F(0,1),易知AB的斜率存在,设AB的方程为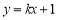 .代入
.代入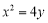 得
得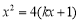 ,即
,即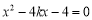 .设
.设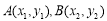 ,则
,则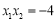 , 2分
, 2分
直线AO的方程为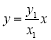 ;BD的方程为
;BD的方程为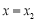 ;解得交点D的坐标为
;解得交点D的坐标为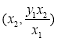 , 4分
, 4分
注意到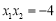 及
及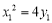 ,则有
,则有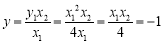 ,
,
因此,D点在定直线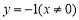 上. 6分
上. 6分
(Ⅱ)设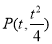 为曲线
为曲线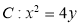 上一点,因为
上一点,因为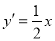 ,所以的斜率为
,所以的斜率为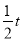 ,因此直线
,因此直线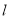 的方程为
的方程为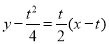 ,即
,即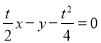 . 8分
. 8分
则Q(0,4)点到的距离 , 10分
, 10分
所以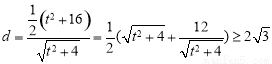
当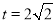 时取等号,所以O点到距离的最小值为
时取等号,所以O点到距离的最小值为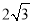 . 13分
. 13分
考点:(1)直线与抛物线的综合问题(2)求最小值.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:2015届豫晋冀高三第二次调研考试文科数学试卷(解析版) 题型:选择题
已知F为抛物线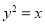 的焦点,点A,B在该抛物线上且位于x轴的两侧,
的焦点,点A,B在该抛物线上且位于x轴的两侧,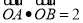 (其中
(其中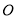 为坐标原点),则
为坐标原点),则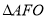 与
与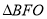 面积之和的最小值是( )
面积之和的最小值是( )
A.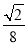 B.
B.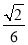 C.
C.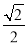 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省文登市高三上学期第一次考试理科数学试卷(解析版) 题型:选择题
已知函数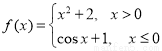 则下列结论正确的是( )
则下列结论正确的是( )
A.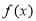 是偶函数 B.
是偶函数 B.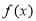 是增函数
是增函数
C.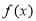 是周期函数 D.
是周期函数 D.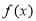 的值域为
的值域为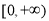
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济宁市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
函数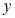 =
=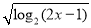 的定义域为( )
的定义域为( )
(A)(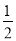 ,
,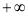 ) (B)[1,
) (B)[1,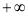
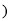 (C)(
(C)(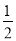 ,1
,1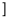 (D)(
(D)(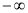 ,1)
,1)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:填空题
某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
韭菜 | 6吨 | 0.9万元 | 0.3万元 |
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:选择题
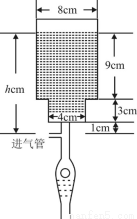
如图所示,医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后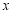 分钟, 瓶内液面与进气管的距离为
分钟, 瓶内液面与进气管的距离为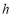 厘米,已知当
厘米,已知当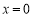 时,
时,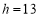 .如果瓶内的药液恰好156分钟滴完. 则函数
.如果瓶内的药液恰好156分钟滴完. 则函数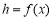 的图像为( )
的图像为( )
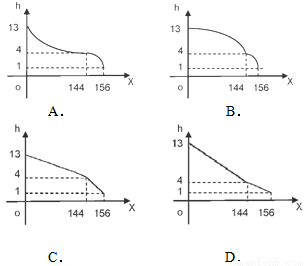
查看答案和解析>>
科目:高中数学 来源:2014-2015学年宁夏银川市高一上学期9月月考数学试卷(解析版) 题型:填空题
下列说法:
① 函数 的单调增区间是
的单调增区间是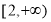 ;
;
② 设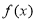 是
是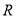 上的任意函数,则
上的任意函数,则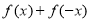 是偶函数,
是偶函数,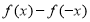 是奇函数;
是奇函数;
③ 已知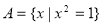 ,
,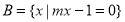 ,若
,若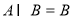 ,则实数
,则实数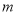 取值集合是
取值集合是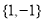 ;
;
④ 函数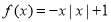 对于定义域
对于定义域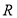 内任意
内任意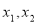 ,当
,当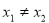 时,恒有
时,恒有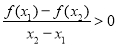 ;
;
⑤ 已知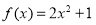 是定义在
是定义在 上的函数,则存在区间I,满足
上的函数,则存在区间I,满足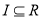 ,使得对于
,使得对于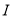 上任意
上任意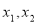 ,当
,当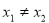 时,恒有
时,恒有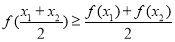 .
.
其中正确的是__________.(只填写相应的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com