等差数列{an}中,已知a1=3,a4=12,
(I)求数列{an}的通项公式;
(Ⅱ)若a2,a4分别为等比数列{bn}的第1项和第2项,试求数列{bn}的通项公式及前n项和Sn.
解:(I)设数列{a
n}的公差为d,
由已知有

(2分)
解得d=3(4分)
∴a
n=3+(n-1)3=3n(6分)
(Ⅱ)由(I)得a
2=6,a
4=12,则b
1=6,b
2=12,(8分)
设b
n的公比为q,则
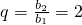
,(9分)
从而b
n=6•2
n-1=3•2
n(11分)
所以数列{b
n}的前n项和
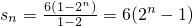
(12分)
分析:(I)求数列{a
n}的通项公式,由等差数列{a
n}中,已知a
1=3,a
4=12,先求出公差d,再依据等差数列的通项公式求其通项即可.
(Ⅱ)若a
2,a
4分别为等比数列{b
n}的第1项和第2项,由此即可求出等比数列的首项与公比,再由公式求出其通项公式及前n项和S
n.
点评:本题考查等差数列与等比数列的综合,熟知等差数列与等比数列的性质是求解本题的关键,本题属于考查基本公式型的题,思维难度相对较低.

 (2分)
(2分)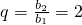 ,(9分)
,(9分)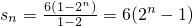 (12分)
(12分)

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案