
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用三棱柱ABC-A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角.利用三棱锥的体积计算公式可得AA1,再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1=$\frac{A{A}_{1}}{{A}_{1}P}$,可得结论.
解答 解:如图所示,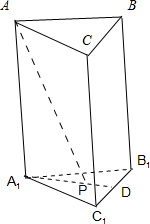
∵AA1⊥底面A1B1C1,∴∠APA1为PA与平面A1B1C1所成角,
∵平面ABC∥平面A1B1C1,∴∠APA1为PA与平面ABC所成角.
∵${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{3\sqrt{3}}{4}$.
∴V三棱柱ABC-A1B1C1=$\frac{3\sqrt{3}}{4}$AA1,解得AA1=$\sqrt{3}$.
又P为底面正三角形A1B1C1的中心,∴A1P=1,
在Rt△AA1P中,tan∠APA1=$\frac{A{A}_{1}}{{A}_{1}P}$=$\sqrt{3}$,
∴∠APA1=60°.
故选B.
点评 本题考查线面角,掌握正三角形的性质、线面角的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
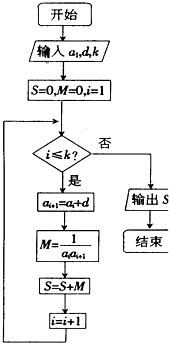 已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1或-\frac{1}{3}$ | B. | $\frac{1}{2}或1$ | C. | 1 | D. | $\frac{1}{2}或-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com