
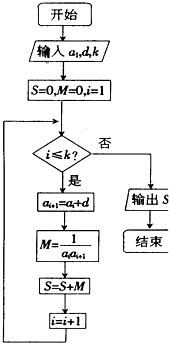
 已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$分析 (1)由框图可知S=$\frac{1}{{a}_{1}{a}_{2}}+\frac{1}{{a}_{2}{a}_{3}}+…+\frac{1}{{a}_{k}{a}_{k+1}}$,$\frac{1}{{a}_{k}{a}_{k+1}}$=$\frac{1}{d}$($\frac{1}{{a}_{k}}+\frac{1}{{a}_{k+1}}$),从而S=$\frac{1}{d}$($\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{k+1}}$),由此能求出数列{an}的通项.
(2)由${b}_{n}={2}^{{a}_{n}}={2}^{2n-1}$,能求出b1+b2+…+b2015的值.
解答 解:(1)由框图可知:
S=$\frac{1}{{a}_{1}{a}_{2}}+\frac{1}{{a}_{2}{a}_{3}}+…+\frac{1}{{a}_{k}{a}_{k+1}}$,
∵{an}是等差数列,设公差为d,
∴$\frac{1}{{a}_{k}{a}_{k+1}}$=$\frac{1}{d}$($\frac{1}{{a}_{k}}+\frac{1}{{a}_{k+1}}$),
∴$S=\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{k}}-\frac{1}{{a}_{k+1}})$=$\frac{1}{d}$($\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{k+1}}$),
由题意可知,k=5时,S=$\frac{5}{11}$,k=10时,$S=\frac{10}{21}$,
∴$\left\{\begin{array}{l}{\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{6}})=\frac{5}{11}}\\{\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{11}})=\frac{10}{21}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$,或$\left\{\begin{array}{l}{{a}_{1}=-1}\\{d=-2}\end{array}\right.$(舍),
∴an=a1+(n-1)d=2n-1.
(2)由(1)得:${b}_{n}={2}^{{a}_{n}}={2}^{2n-1}$,
∴b1+b2+…+b2015
=2+23+…+22n-1
=$\frac{2(1-{4}^{n})}{1-4}$
=$\frac{2}{3}$(4n-1).
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意程序框图的性质的合理运用.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,2} | C. | {1,3} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com