
分析 由f(1)=$\frac{1}{2}$,得2a+b=2,由f(x)=x有一个解,得方程ax2+(b-1)x=0(x≠-$\frac{b}{a}$)有唯一解,由此能求出函数f(x)的解析式和f[f(-3)]的值.
解答 解:∵函数f(x)=$\frac{x}{ax+b}$(a,b是常数且a≠0),
满足f(1)=$\frac{1}{2}$,∴$\frac{2}{2a+b}$=1,
化简得2a+b=2,
又∵f(x)=x有一个解,
∴$\frac{x}{ax+b}$=x有一个解,即方程ax2+(b-1)x=0(x≠-$\frac{b}{a}$)有唯一解
(b-1)2=0,解得:a=$\frac{1}{2}$,b=1,
当x=-$\frac{b}{a}$时,代入上面方程解得a=1,b=0
此时f(x)=x有唯一解,
∴所求为f(x)=$\frac{2x}{x+2}$或f(x)=1(x≠0).
f(-3)=$\frac{2×(-3)}{-3+2}$=6,
f[f(-3)]=f(6)=$\frac{2×6}{6+2}$=$\frac{3}{2}$.
点评 本题考查函数的解析式和函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,2) | C. | (2,3] | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
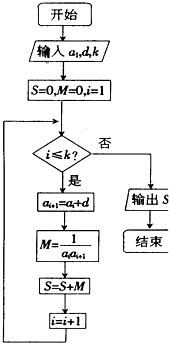 已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=$\frac{5}{11}$和S=$\frac{10}{21}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①③ | C. | ①② | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com