
分析 当直线过原点时斜率存在,设方程为y=kx,当直线不过原点时,设直线的方程为y=a-x,分别联立方程由△=0可得.
解答 解:当直线过原点时斜率存在,设方程为y=kx,
联立直线与圆的方程,消去y可得(k2+1)x2-(4+6k)x+12=0,
由相切可得△=(4+6k)2-48(k2+1)=0,解得k=2±$\frac{2\sqrt{3}}{3}$,
∴所求直线的方程为y=(2±$\frac{2\sqrt{3}}{3}$)x,即$y=\frac{6+2\sqrt{3}}{3}x或y=\frac{6-2\sqrt{3}}{3}x$;
当直线不过原点时,设直线的方程为y=a-x,
联立直线与圆的方程消去y可得2x2-(-1-a)x+a2-6a+11=0,
由相切可得△=(-1-a)2-8(a2-6a+11)=0,解得a=5$±\sqrt{2}$,
∴所求直线的方程为$x+y-5+\sqrt{2}=0$或$x+y-5-\sqrt{2}=0$.
综上可得所求直线的方程为$y=\frac{6+2\sqrt{3}}{3}x或y=\frac{6-2\sqrt{3}}{3}x$或$x+y-5+\sqrt{2}=0$或$x+y-5-\sqrt{2}=0$
点评 本题考查直线与圆的相切关系,涉及分类讨论的思想和一元二次方程的根与判别式的关系,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在斜二测画法下,四边形A′B′C′D′是下底角为45°的等腰梯形,其下底长为5,一腰长为$\sqrt{2}$,则原四边形的面积是( )
如图,在斜二测画法下,四边形A′B′C′D′是下底角为45°的等腰梯形,其下底长为5,一腰长为$\sqrt{2}$,则原四边形的面积是( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{2}{x}$ | B. | f(x)=-x+1 | C. | f(x)=|x-1| | D. | f(x)=2x2+3x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
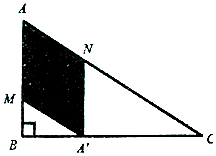 如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.
如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com