
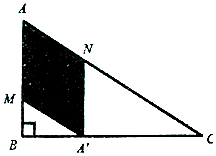
 如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.
如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.分析 由∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a,得∠BAC=$\frac{π}{3}$,设MA=MA′=xa(0<x<1),则MB=a-xa,所以在Rt△MBA′中,cos(π-2θ)=$\frac{a-xa}{xa}$=$\frac{1-x}{x}$;
(1)因为θ=$\frac{π}{3}$,所以cos(π-2θ)=$\frac{1-x}{x}$=$\frac{1}{2}$,解得x值,可得△AMN为等边三角形,进而得到最美绿地的面积;
(2)根据(1)中结论,可得AN=$\frac{a}{\frac{1}{2}+sin(2θ-\frac{π}{6})}$,根据三角函数的图象和性质,可得θ=$\frac{π}{3}$时,AN最短,且AN=$\frac{2}{3}a$,进而得到答案.
解答 解:由∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a,得∠BAC=$\frac{π}{3}$…(1分)
设MA=MA′=xa(0<x<1),则MB=a-xa,
所以在Rt△MBA′中,cos(π-2θ)=$\frac{a-xa}{xa}$=$\frac{1-x}{x}$…(3分)
(1)因为θ=$\frac{π}{3}$,所以cos(π-2θ)=$\frac{1-x}{x}$=$\frac{1}{2}$,所以x=$\frac{2}{3}$,
又∠BAC=$\frac{π}{3}$,所以△AMN为等边三角形,所以绿地的面积S=2×$\frac{1}{2}$×$\frac{2}{3}$a×$\frac{2}{3}$a×sin$\frac{π}{3}$=$\frac{2\sqrt{3}}{9}{a}^{2}$…(5分)
(2)因为cos(π-2θ)═-cos2θ=2sin2θ-1=$\frac{1-x}{x}$,
所以x=$\frac{1}{2{sin}^{2}θ}$,则AM=$\frac{a}{2{sin}^{2}θ}$…(7分)
又∠BAC=$\frac{π}{3}$,所以在△AMN中,∠ANM=$\frac{2π}{3}-θ$,故$\frac{AN}{sinθ}=\frac{AM}{sin(\frac{2π}{3}-θ)}$,
所以AN=$\frac{a}{2{sin}^{2}θ}$×$\frac{sinθ}{sin(\frac{2π}{3}-θ)}$=$\frac{a}{2sinθ•sin(\frac{2π}{3}-θ)}$=$\frac{a}{\frac{1}{2}+sin(2θ-\frac{π}{6})}$…(11分)
又$\frac{π}{4}<θ<\frac{π}{2}$,所以$\frac{π}{3}<2θ-\frac{π}{6}<\frac{5π}{6}$,
所以当$2θ-\frac{π}{6}=\frac{π}{2}$,即θ=$\frac{π}{3}$时,AN最短,且AN=$\frac{2}{3}a$,
此时公共绿地走道MN=$\frac{2}{3}a$…(12分)
点评 本题考查的知识点是函数的应用,函数的最值,熟练掌握三角函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1或-\frac{1}{3}$ | B. | $\frac{1}{2}或1$ | C. | 1 | D. | $\frac{1}{2}或-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=A | B. | A⊆B | C. | A∩B=∅ | D. | A∩(∁IB)≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | $\frac{9}{19}$ | C. | $\frac{11}{23}$ | D. | $\frac{9}{23}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com