练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．设Sn，Tn分别是等差数列{an}，{bn}的前n项和，若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{2n+1}$（n∈N*），则$\frac{{a}_{6}}{{b}_{6}}$=（　　）
    A．$\frac{5}{13}$B．$\frac{9}{19}$C．$\frac{11}{23}$D．$\frac{9}{23}$

    分析 由等差数列的性质和求和公式进行解答．

    解答 解：由等差数列的性质和求和公式可得：$\frac{{a}_{6}}{{b}_{6}}$=$\frac{{2a}_{6}}{{2b}_{6}}$=$\frac{\frac{11}{2}（{a}_{1}+{a}_{11}）}{\frac{11}{2}（{b}_{1}+{b}_{11}）}$=$\frac{{S}_{11}}{{T}_{11}}$=$\frac{11}{2×11+1}$=$\frac{11}{23}$．
    故选：C．

    点评 本题考查等差数列的性质和求和公式，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

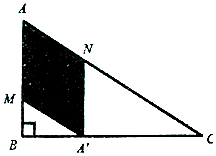    20．如图，某小区准备将一块闲置的直角三角形（其中∠B=$\frac{π}{2}$，AB=a，BV=$\sqrt{3}$a）土地开发成公共绿地，设计时，要求绿地部分（图中阴影部分）有公共绿地走道MN，且两边是两个关于走道MN对称的三角形（△AMN和△A′MN），现考虑方便和绿地最大化原则，要求M点与B点不重合，A′点落在边BC上，设∠AMN=θ．
    （1）若θ=$\frac{π}{3}$，绿地“最美”，求最美绿地的面积；
    （2）为方便小区居民行走，设计时要求AN，A′N最短，求此时公共绿地走道MN的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．正方体ABCD-A1B1C1D1中，若$\overrightarrow{A{C_1}}$=x（$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C_1}}$），则实数x=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合A={0，1，2，3，4，5}，B={1，3，6，9}，C={3，7，8}，则（A∩B）∪C=（
    A．{3}B．{3，7，8}C．{1，3，7，8}D．{1，3，6，7，8}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．把函数y=sinx（x∈R）的图象上所有的点向左平行移动$\frac{π}{6}$个单位长度，再把所得图象上所有点的横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变），得到的图象所表示的函数是（　　）
    A．$y=sin（2x-\frac{π}{6}）$，x∈RB．$y=sin（\frac{x}{2}+\frac{π}{12}）$，x∈RC．$y=sin（2x+\frac{π}{6}）$，x∈RD．$y=sin（2x+\frac{π}{3}）$，x∈R

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．设0＜a≤1，函数f（x）=x+$\frac{a}{x}$-1，g（x）=x-2lnx，若对任意的x1∈[1，e]，存在x2∈[1，e]都有f（x1）≥g（x2）成立，则实数a的取值范围是[2-2ln2，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若（x2+$\frac{1}{x}$）n的二项展开式中，所以二项式系数之和为64，则n=6；该展开式中的常数项为15（用数字作答）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列各函数中，表示同一函数的是（　　）
    A．y=lgx与$y=\frac{1}{2}lgx{\;}^2$B．$y=\frac{{{x^2}-1}}{x-1}$与y=x+1
    C．$y=\sqrt{x^2}-1$与y=x-1D．y=x与$y={log_a}{a^x}$（a＞0且a≠1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．数列{an}的首项a1=1，an+1=an+2n，则a5=（　　）
    A．$\frac{45}{2}$B．20C．21D．31

    查看答案和解析>>

    同步练习册答案