
分析 求出原函数的导函数,由题意列式求得a值.
(1)分别由导函数大于0和导函数小于0求得原函数的单调区间;
(2)把kf(s)≥t ln t在s∈(0,+∞),t∈(1,e]上恒成立,转化为k≥$\frac{tlnt}{f(s)}$在s∈(0,+∞),t∈(1,e]上恒成立,即k≥$[\frac{tlnt}{f(s)}]_{max}$恒成立.利用导数分别求出f(x)在(0,+∞)上的最小值和g(x)在(1,e]上的最大值得答案.
解答 解:由f(x)=e2x+$\frac{1}{ax}$,得f′(x)=e2-$\frac{1}{a{x}^{2}}$,
∴f′(1)=${e}^{2}-\frac{1}{a}$,则${e}^{2}-\frac{1}{a}$=e2-1,得a=1.
∴f(x)=e2x+$\frac{1}{x}$,f′(x)=e2-$\frac{1}{{x}^{2}}$,
(1)由f′(x)=e2-$\frac{1}{{x}^{2}}$>0,得x$<-\frac{1}{e}$或x>$\frac{1}{e}$,
由f′(x)=e2-$\frac{1}{{x}^{2}}$<0,得$-\frac{1}{e}$<x<$\frac{1}{e}$且x≠0,
∴f(x)的单调增区间为(-∞,-$\frac{1}{e}$),($\frac{1}{e}$,+∞).
单调减区间为($-\frac{1}{e},0$),(0,$\frac{1}{e}$);
(2)当s∈(0,+∞),t∈(1,e]时,f(s)>0,t ln t>0,
由kf(s)≥t ln t,可得k≥$\frac{tlnt}{f(s)}$在s∈(0,+∞),t∈(1,e]上恒成立,
即k≥$[\frac{tlnt}{f(s)}]_{max}$恒成立.
设g(x)=xlnx,故只需求出f(x)在(0,+∞)上的最小值和g(x)在(1,e]上的最大值,
由(1)知,f(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,
故f(x)在(0,+∞)上的最小值为f($\frac{1}{e}$)=${e}^{2}•\frac{1}{e}+e=2e$,
由g(x)=xlnx,可得g′(x)=lnx+1,当x∈(1,e]时,g′(x)>0,
∴g(x)在(1,e]上单调递增,g(x)的最大值为g(e)=e.
∴只需k≥$\frac{e}{2e}=\frac{1}{2}$.
∴实数k的取值范围是[$\frac{1}{2}$,+∞).
点评 本题主要考查不等式恒成立、函数的最值、导数的几何意义等知识,意在考查考生综合运用所学知识分析问题、解决问题的能力,属压轴题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | 表示某同学参加高考报名的程序 | |
| B. | 表示某企业生产某种产品的生产工序 | |
| C. | 表示某图书馆的图书借阅程序 | |
| D. | 表示某单位的各部门的分工情况 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{2}{x}$ | B. | f(x)=-x+1 | C. | f(x)=|x-1| | D. | f(x)=2x2+3x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
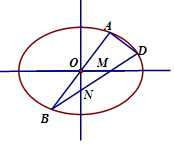 对于椭圆C,$\frac{x{\;}^{2}}{8}$+$\frac{y{\;}^{2}}{4}$=1,过原点的直线与椭圆C交于A,B两点(非顶点),
对于椭圆C,$\frac{x{\;}^{2}}{8}$+$\frac{y{\;}^{2}}{4}$=1,过原点的直线与椭圆C交于A,B两点(非顶点),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
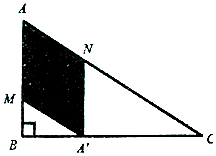 如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.
如图,某小区准备将一块闲置的直角三角形(其中∠B=$\frac{π}{2}$,AB=a,BV=$\sqrt{3}$a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{10}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com