
【题目】已知圆M的圆心M在y轴上,半径为1.直线l:y=2x+2被圆M所截得的弦长为 ![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(1)求圆M的方程;
(2)设A(t,0),B(t+5,0)(﹣4≤t≤﹣1),若AC,BC是圆M的切线,求△ABC面积的最小值.
【答案】
(1)解:设M(0,b)由题设知,M到直线l的距离是 ![]() =
= ![]()
所以 ![]() =
= ![]() ,解得b=1或b=3
,解得b=1或b=3
因为圆心M在直线l的下方,所以b=1,
即所求圆M的方程为x2+(y﹣1)2=1
(2)解:当直线AC,BC的斜率都存在,即﹣4<t<﹣1时
直线AC的斜率kAC=tan2∠MAO= ![]() =
= ![]() ,
,
同理直线BC的斜率kBC= ![]()
所以直线AC的方程为y= ![]() (x﹣t),
(x﹣t),
直线BC的方程为y= ![]() (x﹣t﹣5)
(x﹣t﹣5)
解方程组 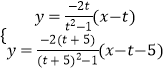
得x= ![]() ,y=
,y= ![]()
所以y= ![]() =2﹣
=2﹣ ![]()
因为﹣4≤t≤﹣1
所以﹣ ![]() ≤t2+5t+1<﹣3
≤t2+5t+1<﹣3
所以 ![]() ≤y<
≤y< ![]() .
.
故当t=﹣ ![]() 时,△ABC的面积取最小值
时,△ABC的面积取最小值 ![]() ×5×
×5× ![]() =
= ![]() .
.
当直线AC,BC的斜率有一个不存在时,即t=﹣4或t=﹣1时,易求得△ABC的面积为 ![]() .
.
综上,当t=﹣ ![]() 时,△ABC的面积的最小值为
时,△ABC的面积的最小值为 ![]() .
.
【解析】(1)先设点M的坐标,再根据弦长可得点M到直线l的距离,进而可得b的值,从而可得圆M的方程;(2)当直线AC,BC的斜率都存在时,由已知条件可得直线AC和直线BC的方程,解方程组可得点C的坐标,进而可得△ABC面积,从而可得△ABC面积的最小值,当直线AC,BC的斜率有一个不存在时,易得△ABC面积,综上所述,可得△ABC的面积的最小值.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)我们把一系列向量![]() 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作![]() ,已知向量列
,已知向量列![]() 满足:
满足:![]() ,
,![]()
![]() .
.
(1)证明:数列![]() 是等比数列;
是等比数列;
(2)设![]() 表示向量
表示向量![]() 与
与![]() 间的夹角,若
间的夹角,若![]() ,对于任意正整数
,对于任意正整数![]() ,不等式
,不等式 恒成立,求实数
恒成立,求实数![]() 的范围
的范围
(3)设![]() ,问数列
,问数列![]() 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(2,1)的直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(1)求曲线C的直角坐标方程;
(2)求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.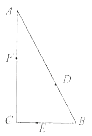
(1)若甲、乙都以每分钟100m的速度从点B出发在各自的大道上奔走,到大道的另一端时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设∠CEF=θ,乙丙之间的距离是甲乙之间距离的2倍,且∠DEF= ![]() ,请将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
,请将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() 得到数对
得到数对![]() .
.
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 在
在![]() 内是偶函数的概率;
内是偶函数的概率;
(2)若![]() ,
, ![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(3)若![]() ,
, ![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=. ![]() ,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,给出下列四个命题:
①若|z1﹣z2|=0,则 ![]() =
= ![]() ②若z1=
②若z1= ![]() ,则
,则 ![]() =z2
=z2
③若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]() ④若|z1|=|z2|,则z12=z22
④若|z1|=|z2|,则z12=z22
其中真命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com