
���� ��1��������ɵ�ab=2�����ɵ㵽ֱ�ߵľ��빫ʽ���ɵ�a2+b2=5���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2����A��x1��y1����B��x2��y2������ֱ�ߴ�����Բ���̣���ȥy���ã�1+4k2��x2+8kmx+4m2-4=0���ɴ����ø����б�ʽ��Τ�ﶨ�����е����깫ʽ������֪������m��0������|x1-x2|���ɴ��������AOB��������ⷽ�̿ɵ�����
��� �⣺��1��ֱ��C1��$\frac{x}{a}$+$\frac{y}{b}$=1��������Ľ���Ϊ��a��0������0��b����
����$\frac{1}{2}$ab=1����ab=2��
��ԭ�㵽ֱ�ߵľ���Ϊ$\frac{2}{\sqrt{5}}$��
��Ϊ$\frac{1}{\sqrt{\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}}}$=$\frac{2}{\sqrt{5}}$��
���a=2��b=1��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1��
��2����A��x1��y1����B��x2��y2����
��ֱ��y=kx+m������Բ���̣���ȥy���ã�1+4k2��x2+8kmx+4m2-4=0��
��x1+x2=$\frac{-8km}{1+4{k}^{2}}$��x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$��
��y1+y2=k��x1+x2��+2m=$\frac{2m}{1+4{k}^{2}}$��
�����е����깫ʽ����G��$\frac{-4km}{1+4{k}^{2}}$��$\frac{m}{1+4{k}^{2}}$����
��Q��$\frac{-4��km}{1+4{k}^{2}}$��$\frac{��m}{1+4{k}^{2}}$��������Բ���̣����æ�2m2=1+4k2���ڣ�
�ڽ⣺�ɢ٢ڵ�m��0���ˣ�1��|x1-x2|=$\frac{4\sqrt{1+4{k}^{2}-{m}^{2}}}{1+4{k}^{2}}$����
��Ϣڢۣ���S��AOB=$\frac{1}{2}$|m|•|x1-x2|=$\frac{2\sqrt{{��}^{2}-1}}{{��}^{2}}$���ˡʣ�1��+�ޣ���
��S��AOB=1����æ�=$\sqrt{2}$��
���� ���⿼����Բ�ķ��̺����ʣ�����ֱ�ߺ���Բ��λ�ù�ϵ��ֱ�߷��̺���Բ��������������Τ�ﶨ����ͬʱ���������Ĺ��ߵ������ʾ�������ε������ʽ�����ã������е��⣮


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
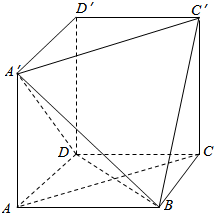 �ڳ�����ABCD-A��B��C��D���У�AB=BC=2����A�䣬C�䣬B�����ƽ���ȥ�������һ���Ǻõ�ABCD-A��C��D�䣬
�ڳ�����ABCD-A��B��C��D���У�AB=BC=2����A�䣬C�䣬B�����ƽ���ȥ�������һ���Ǻõ�ABCD-A��C��D�䣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
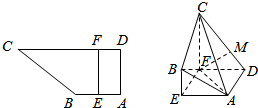 ��ͼ��ʾ���ı���ABCD�У���BAD=��ADC=90�㣬AB=AD=$\frac{1}{2}$CD=2����E�ڱ�AB�ϣ���F�ڱ�CD�ϣ���EF��AD����EF����EBCF����ʹ��CF��AE��
��ͼ��ʾ���ı���ABCD�У���BAD=��ADC=90�㣬AB=AD=$\frac{1}{2}$CD=2����E�ڱ�AB�ϣ���F�ڱ�CD�ϣ���EF��AD����EF����EBCF����ʹ��CF��AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD-A1B1C1D1�У�E����B1C1���е㣬����PΪ����������ϵ���һ�㣮
��ͼ��������ABCD-A1B1C1D1�У�E����B1C1���е㣬����PΪ����������ϵ���һ�㣮| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com