
【题目】如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE= ![]() ,∠EAD=∠EAB.
,∠EAD=∠EAB. 
(1)证明:平面ACEF⊥平面ABCD;
(2)若AE与平面ABCD所成角为60°,求二面角B﹣EF﹣D的余弦值.
【答案】
(1)证明:连接EG,
∵四边形ABCD为菱形,∴AD=AB,BD⊥AC,DG=GB,
在△EAD和△EAB中,
AD=AB,AE=AE,∠EAD=∠EAB,
∴△EAD≌△EAB,
∴ED=EB,则BD⊥EG,
又AC∩EG=G,∴BD⊥平面ACEF,
∵BD平面ABCD,
∴平面ACEF⊥平面ABCD
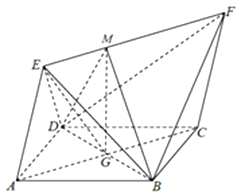
(2)解法一:过G作EF的垂线,垂足为M,连接MB,MG,MD,
易得∠EAC为AE与面ABCD所成的角,
∴∠EAC=60°,
∵EF⊥GM,EF⊥BD,
∴EF⊥平面BDM,
∴∠DMB为二面角B﹣EF﹣D的平面角,
可求得MG= ![]() ,DM=BM=
,DM=BM= ![]() ,
,
在△DMB中,由余弦定理可得:cos∠BMD= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() ;
;
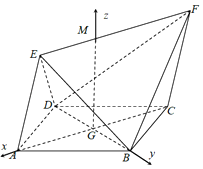
解法二:如图,在平面ABCD内,过G作AC的垂线,交EF于M点,
由(1)可知,平面ACEF⊥平面ABCD,
∵MG⊥平面ABCD,
∴直线GM、GA、GB两两互相垂直,
分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,
可得∠EAC为AE与平面ABCD所成的角,∴∠EAC=60°,
则D(0,﹣1,0),B(0,1,0),E( ![]() ),F(
),F( ![]() ),
),
![]() ,
, ![]() ,
,
设平面BEF的一个法向量为 ![]() ,则
,则
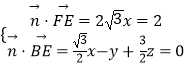 ,
,
取z=2,可得平面BEF的一个法向量为 ![]() ,
,
同理可求得平面DEF的一个法向量为 ![]() ,
,
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() .
.
【解析】(1)连接EG,由四边形ABCD为菱形,可得AD=AB,BD⊥AC,DG=GB,可证△EAD≌△EAB,进一步证明BD⊥平面ACEF,则平面ACEF⊥平面ABCD;(2)法一、过G作EF的垂线,垂足为M,连接MB,MG,MD,可得∠EAC为AE与面ABCD所成的角,得到EF⊥平面BDM,可得∠DMB为二面角B﹣EF﹣D的平面角,在△DMB中,由余弦定理求得∠BMD的余弦值,进一步得到二面角B﹣EF﹣D的余弦值;法二、在平面ABCD内,过G作AC的垂线,交EF于M点,由(1)可知,平面ACEF⊥平面ABCD,得MG⊥平面ABCD,则直线GM、GA、GB两两互相垂直,分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,分别求出平面BEF与平面DEF的一个法向量,由两法向量所成角的余弦值可得二面角B﹣EF﹣D的余弦值.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),当x∈[0,2]时,f(x)=4(1﹣|x﹣1|),且对于任意实数x∈[2n﹣2,2n+1﹣2](n∈N* , n≥2),都有f(x)= ![]() f(
f( ![]() ﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
A.[2,10]
B.[ ![]() ,
, ![]() ]
]
C.(2,10)
D.[2,10)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个简单几何体的正视图、侧视图如图所示,则其俯视图可能是( )
①长、宽不相等的长方形 ②正方形 ③圆 ④椭圆.
A.①②
B.①④
C.②③
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1 , CC1=B1C1=2BB1=2,D是CC1的中点.四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到,且二面角B1﹣CC1﹣A为120°. 
(1)若点E是线段A1B1上的动点,求证:DE∥平面ABC;
(2)求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:kx+y+4=0(k∈R)是圆C:x2+y2+4x﹣4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线m,则直线m被圆C所截得的弦长为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线
(α为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线 ![]() .
.
(Ⅰ)写出曲线C1 , C2的普通方程;
(Ⅱ)过曲线C1的左焦点且倾斜角为 ![]() 的直线l交曲线C2于A,B两点,求|AB|.
的直线l交曲线C2于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)写出C1的普通方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com