
 是圆
是圆 上任意一点,点
上任意一点,点 与点
与点 关于原点对称.线段
关于原点对称.线段 的中垂线
的中垂线 分别与
分别与 交于
交于 两点.
两点. 的轨迹
的轨迹 的方程;
的方程; 与曲线
与曲线 交于
交于 两点,若
两点,若 (
( 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.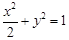 ;(2)
;(2)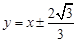
 是圆
是圆 上任意一点,点
上任意一点,点 与点
与点 关于
关于 的中垂线
的中垂线 分别与
分别与 交于
交于 两点.利用定义法得到轨迹方程。
两点.利用定义法得到轨迹方程。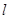 的方程为
的方程为 ,由
,由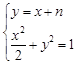 ,联立方程组,结合韦达定理得到根与系数的关系,进一步结合向量的数量积为零得到结论。
,联立方程组,结合韦达定理得到根与系数的关系,进一步结合向量的数量积为零得到结论。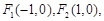 圆
圆 的半径为
的半径为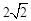 ,且
,且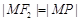 … 1分
… 1分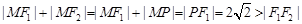 …………………………… 3分
…………………………… 3分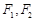 为焦点的椭圆, ………………………………………… 5分
为焦点的椭圆, ………………………………………… 5分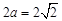 ,得到
,得到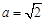 ,焦距
,焦距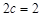 ,则短半轴
,则短半轴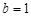
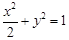 ………………………………………………………… 6分
………………………………………………………… 6分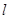 的方程为
的方程为 ,由
,由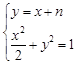
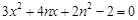 …………………………………………………………… 8分
…………………………………………………………… 8分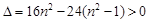 ,即
,即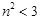 ① …………………………………9分
① …………………………………9分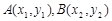 ,则
,则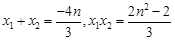
 可得
可得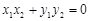 ,即
,即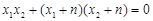 …………………10分
…………………10分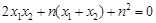
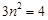 ,满足①式,故直线
,满足①式,故直线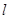 的方程为:
的方程为: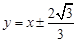 …………………12分
…………………12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 ,动点N在圆
,动点N在圆 上运动,线段MN的
上运动,线段MN的 与点P的轨迹相切,且
与点P的轨迹相切,且 在
在 轴.
轴. 轴上的截距相等,求直线
轴上的截距相等,求直线 的方程.
的方程. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com