Question

设函数y=f（x）是定义在R上的函数，当x＜0时，f（x）＞1，对任意实数x、y∈R，有?f（x+y）=f（x）·f（y）.?

（1）求证：f（0）=1，且当x＞0时，有0＜f（x）＜1.

（2）若数列｛a_n｝满足a₁=f（0），且f（a_n+1）=，n∈N^*.

①求a_n；

②若不等式（1+）（1+）…（1+）≥k·，对于n∈N^*都成立，求k的最大值.

Answer 1

（1）证明:∵x、y∈R,有f（x+y）=f（x）·f（y）,

∴取y=0，x＜0,则f（x）=f（x）f（0）x＜0时f（x）＞1，∴f（0）=1.

又设x＞0，y=-x＜0，则1=f（0）=f（x）f（-x），

∴f（x）=.

而当-x＜0时，f（-x）＞1，∴当x＞0时，0＜f（x）＜1．                        

（2）解:①｛a_n｝中，a₁=f（0）=1，由f（a_n+1）=,得f（a_n+1）f（-a_n-2）=1=f（0），

∴f（a_n+1-a_n-2）=f（0）.                                                     

可证y=f（x）是R上的递减函数，证明如下：

设x₁、x₂∈R且x₁＜x₂，则x₂=x₁+t（t＞0），f（t）∈（0，1）.

∴f（x₂）=f（x₁+t）=f（x₁）f（t）＜f（x₁），即?f（x₂）＜f（x₁）.∴f（x）是R上的减函数.

∴?a_n+1-a_n-2=0，即a_n+1-a_n=2.∴a_n=2n-1.                                       

②设g（n）=，得.

∴＜1.

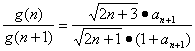∴＜1，即g（n）＜g（n+1）.

∴g（n）对n∈N^*单调递增.而k≤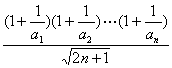恒成立，

即k≤g（n）对n∈N^*恒成立.∴k≤g（1）=，即k≤.∴k的最大值为.