
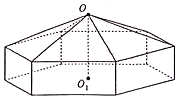
 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?  解:设OO1为xm,
解:设OO1为xm,| 32-(x-1)2 |
| 8+2x-x2 |
| 32-(x-1)2 |
| ||
| 4 |
| 8+2x-x2 |
3
| ||
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
(06年江苏卷)(14分)
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正
六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心![]() 的距离为多少时,帐篷的体积最
的距离为多少时,帐篷的体积最
大?

查看答案和解析>>
科目:高中数学 来源: 题型:
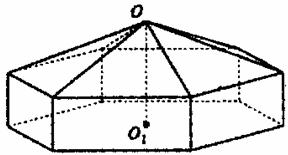
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心![]() 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:选修2-2综合测试(解析版) 题型:解答题
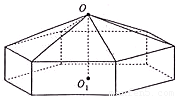 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com