若圆C:x2+y2-ax+2y+1=0和圆x2+y2=1关于直线y=x-1对称,动圆P与圆C相外切且直线x=-1相切,则动圆圆心P的轨迹方程是( )
A.y2+6x-2y+2=0
B.y2-2x+2y=0
C.y2-6x+2y-2=0
D.y2-2x+2y-2=0
【答案】
分析:求出两个圆的圆心坐标,两个半径,利用两个圆关于直线的对称知识,求出a的值,设圆心P到直线x=-1的距离等于r,则由题意有可得 PC=1+r,即
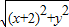
=1+x+1,化简可得 P 的轨迹方程.
解答:解:圆x
2+y
2-ax+2y+1=0的圆心(
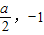
),
因为圆x
2+y
2-ax+2y+1=0与圆x
2+y
2=1关于直线y=x-1对称,
所以(
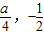
)满足直线y=x-1方程,解得a=2,
设圆心P到直线x=1的距离等于r,P(x,y ),则由题意有可得 PC=1+r,
即
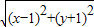
=1+1+x,化简可得 y
2-6x+2y-2=0,
故选C.
点评:本题是中档题,考查圆关于直线对称的圆的方程,动圆圆心的轨迹方程问题,考查转化思想,按照轨迹方程求法步骤解答,是常考题.

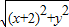 =1+x+1,化简可得 P 的轨迹方程.
=1+x+1,化简可得 P 的轨迹方程.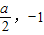 ),
),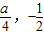 )满足直线y=x-1方程,解得a=2,
)满足直线y=x-1方程,解得a=2,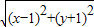 =1+1+x,化简可得 y2-6x+2y-2=0,
=1+1+x,化简可得 y2-6x+2y-2=0,
