
分析 (1)用二倍角的余弦公式变形、两角和的正弦公式化简解析式,求出f($\frac{π}{4}$)的值;
(2)由x的范围和正弦函数的图象与性质求出f(x)的值域;
(3)由(1)求出f(4x)的解析式,由正弦函数的对称轴方程列出方程化简,由x0∈[0,$\frac{π}{4}$]求出x0的值.
解答 解:(1)由题意得,f(x)=sinx-cosx-1=$\sqrt{2}sin(x-\frac{π}{4})-1$,
所以f($\frac{π}{4}$)=$\sqrt{2}sin(\frac{π}{4}-\frac{π}{4})-1$=-1; …(2分)
(2)由(1)得,f(x)=$\sqrt{2}sin(x-\frac{π}{4})-1$…(3分)
由x∈[0,π]得x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],则$\sqrt{2}sin(x-\frac{π}{4})∈[-\frac{\sqrt{2}}{2},1]$…(4分)
则$\sqrt{2}sin(x-\frac{π}{4})-1∈[-2,\sqrt{2}-1]$
所以值域为[-2,$\sqrt{2}-1$]…(6分)
(3)由(1)得,y=f(4x)=$\sqrt{2}sin(4x-\frac{π}{4})-1$,…(7分)
令$sin(x-\frac{π}{4})=±1$ 得,$4x-\frac{π}{4}=kπ+\frac{π}{2}(k∈Z)$…(9分)
解得$x=\frac{kπ}{4}+\frac{3π}{16}(k∈Z)$,
由$0≤\frac{kπ}{4}+\frac{3π}{16}≤\frac{π}{4}$ (k∈Z)得k=0…(11分)
因此${x}_{0}=\frac{3π}{16}$…(12分)
点评 本题考查正弦函数的图象与性质,二倍角的余弦公式变形、两角和的正弦公式,考查整体思想,化简、变形能力.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | t | 70 |
| A. | 50 | B. | 55 | C. | 56.5 | D. | 55.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
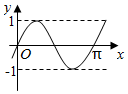 已知函数f(x)=sinωx(ω>0)的部分图象如图所示,为得到函数y=cos(ωx+$\frac{π}{3}$)的图象,只需将函数y=f(x)的图象( )
已知函数f(x)=sinωx(ω>0)的部分图象如图所示,为得到函数y=cos(ωx+$\frac{π}{3}$)的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{5π}{6}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com