
已知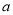 是实数,函数
是实数,函数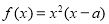 .
.
(1)若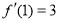 ,求
,求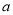 的值及曲线
的值及曲线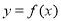 在点
在点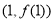 处的切线方程.
处的切线方程.
(2)求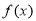 在
在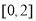 上的最大值.
上的最大值.
(1) ,
,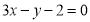 ;(2)
;(2) .
.
【解析】
试题分析:
解题思路:(1)先求导,进而求得 值,利用导数的几何意义求切线方程;(2)求导,讨论
值,利用导数的几何意义求切线方程;(2)求导,讨论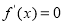 的根与区间
的根与区间 的关系,进而求得极值.
的关系,进而求得极值.
规律总结:导数的几何意义求切线方程: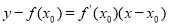 ;利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
;利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
试题解析:(1)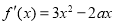 ,因为
,因为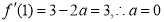
又当 时
时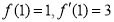
所以曲线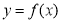 在
在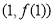 处的切线方程为
处的切线方程为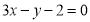
(2)令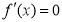 ,解得
,解得 ,
,
当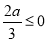 即
即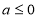 时,
时, 在
在 上单调递增,从而
上单调递增,从而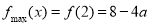 .
.
当 即
即 时,
时, 在
在 上单调递减,从而
上单调递减,从而
当 即
即 时,
时, 在
在 上单调递减,
上单调递减,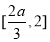 在单调递增,
在单调递增,
从而
综上所述 .
.
考点:1.导数的几何意义;2.利用导数研究函数的最值.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中,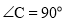 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,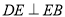 .
.
(1)求证:AC是△BDE的外接圆的切线;
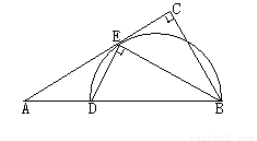
(2)若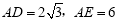 ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知一个扇形弧长为6,扇形圆心角为2rad,则扇形的面积为 ( )
A.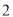 B.3 C.6 D.9
B.3 C.6 D.9
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知三个互不重合的平面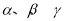 且
且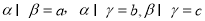 ,给出下列命题:
,给出下列命题:
①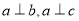 则
则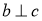 ②
②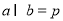 则
则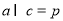 [来源:Z
[来源:Z
③若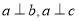 则
则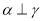 ④若
④若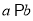 则
则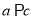
其中正确命题的个数为( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知△ABC中,∠ABC=600,AB=2,BC=6,在BC上任取一点D,则使△ABD为钝角三角形的概率为______________.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
若三棱锥的三个侧面两两垂直,且侧棱长均为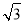 ,则其外接球的表面积为( ).
,则其外接球的表面积为( ).
A.18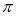 B.36
B.36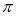 C.9
C.9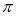 D.
D.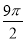
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标模块练习卷(解析版) 题型:填空题
某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com