
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{3}{4}$x | D. | y=$±\frac{4}{3}$x |
分析 通过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{4}$=1(a>0)的实轴长、虚轴长、焦距长成等差数列,求出a,然后求解双曲线的渐近线方程即可.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{4}$=1(a>0)的实轴长2a、虚轴长:4、焦距长2$\sqrt{{a}^{2}+4}$,成等差数列,
所以:8=2a+2$\sqrt{{a}^{2}+4}$,解得a=$\frac{3}{2}$.
双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{4}$=1的渐近线方程为:y=±$\frac{4}{3}$x.
故选:D.
点评 本题考查双曲线的简单性质,考查双曲线的渐近线方程,属于中档题.


科目:高中数学 来源: 题型:选择题
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | 4 |
| 第2行 | 8 | 7 | 6 | 5 |
| 第3行 | 9 | 10 | 11 | 12 |
| 第4行 | 16 | 15 | 14 | 13 |
| … | … | … | … | … |
| A. | 第25行,第1列 | B. | 第25行,第4列 | C. | 第26行,第1列 | D. | 第26行,第4列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
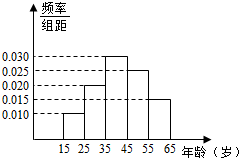 某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:
某电视台为宣传海南,随机对海南15~65岁的人群抽取了n人,回答问题“东环铁路沿线有哪几个城市?”统计结果如图表所示:| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) | a | 0.5 |
| 第2组 | [25,35) | 18 | x |
| 第3组 | [35,45) | b | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 30 | C. | 45 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com