
圆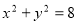 内有一点
内有一点 ,
,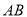 为过点
为过点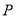 且倾斜角为
且倾斜角为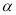 的弦,
的弦,
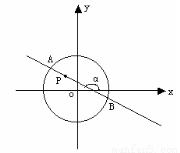
(1)当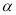 =1350时,求
=1350时,求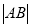 ;
;
(2)当弦 被点
被点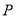 平分时,求出直线
平分时,求出直线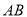 的方程;
的方程;
(3)设过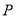 点的弦的中点为
点的弦的中点为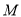 ,求点
,求点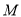 的坐标所满足的关系式.
的坐标所满足的关系式.
(1)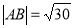 (2)
(2) 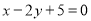 (3)
(3) 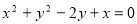
【解析】
试题分析:(1)要求弦长,可利用弦长公式,即将弦所在的直线方程,与圆的方程联立,之后所得的二次方程中,利用 求之.还可以利用圆中
求之.还可以利用圆中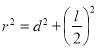 求之,其中
求之,其中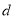 是圆心到弦所在直线的距离,
是圆心到弦所在直线的距离,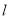 指弦长.但是不论采取哪种方法,都先得求出弦所在的直线方程.根据题意,点斜式可求出.
指弦长.但是不论采取哪种方法,都先得求出弦所在的直线方程.根据题意,点斜式可求出.
(2)当弦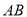 被
被 平分时,弦
平分时,弦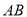 所在直线被直线
所在直线被直线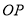 垂直且平分.所以,可先求出直线
垂直且平分.所以,可先求出直线 斜率, 根据垂直可知直线
斜率, 根据垂直可知直线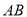 斜率,又因为直线
斜率,又因为直线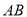 过点
过点 ,根据点斜式可求出直线
,根据点斜式可求出直线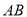 .
.
(3)因为过点 的弦可分为三种情况,①无斜率,此时
的弦可分为三种情况,①无斜率,此时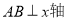 ,
,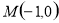 ;②斜率为0,此时
;②斜率为0,此时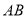 平行x轴,
平行x轴,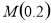 ;③直线
;③直线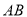 有斜率,且不为0,此时
有斜率,且不为0,此时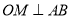 ,根据斜率相乘等于-1可找到
,根据斜率相乘等于-1可找到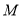 点轨迹,将①②代入③中验证即可.
点轨迹,将①②代入③中验证即可.
试题解析:(1)当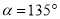 时,直线
时,直线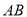 的斜率为-1,根据点斜式有,直线
的斜率为-1,根据点斜式有,直线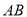 的方程
的方程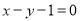 ,
,
所以圆心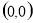 到直线
到直线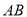 的距离为
的距离为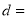
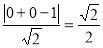 ,又因为
,又因为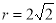 ,
,
所以根据 ,解得
,解得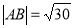

(2)当弦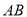 被
被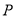 平分时,
平分时,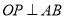 ,
,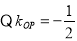 ,
,
又因为直线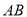 过点
过点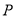 ,所以根据点斜式有直线
,所以根据点斜式有直线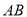 的方程为
的方程为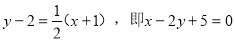 .
.
(3)设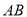 的中点为
的中点为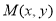 ,则
,则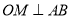 ,即
,即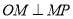
当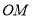 的斜率和
的斜率和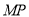 的斜率都存在时:有
的斜率都存在时:有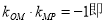
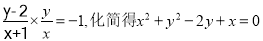
当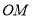 斜率不存在时点
斜率不存在时点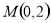 满足上式,
满足上式,
当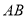 斜率不存在时点
斜率不存在时点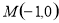 亦满足上式,
亦满足上式,
所以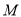 点的轨迹为
点的轨迹为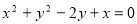 。
。
考点:求圆中的弦长;点斜式求直线;讨论直线斜率情况求点的轨迹.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源:2016届广东省梅州市高一上学期质检数学试卷(解析版) 题型:选择题
一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是( )

查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第二次阶段考数学试卷(解析版) 题型:填空题
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的中位数分别为 和 .

查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第二次阶段考数学试卷(解析版) 题型:选择题
设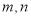 是不同的直线,
是不同的直线, 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
① ②
②
③ ④
④
其中,真命题是( )
A. ①④ B. ②③ C.①③ D. ②④
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第一次阶段考试数学试卷(解析版) 题型:选择题
过点 的直线,将圆形区域
的直线,将圆形区域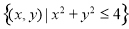 分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届广东省揭阳一中高一下学期期中学业水平测试数学试卷(解析版) 题型:选择题
以下四个命题中,正确的有几个( )
①直线a,b与平面a所成角相等,则a∥b;②两直线a∥b,直线a∥平面a,则必有b∥平面a;③ 一直线与平面的一斜线在平面a内的射影垂直,则该直线必与斜线垂直;④两点A,B与平面a的距离相等,则直线AB∥平面a
A 0个 B 1个 C 2个 D 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com