
已知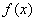 是定义在R上的偶函数,且
是定义在R上的偶函数,且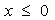 时,
时,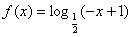 .
.
(Ⅰ)求函数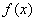 的解析式;
的解析式;
(Ⅱ)若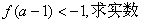
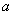 的取值范围.
的取值范围.
解:(Ⅰ)令x>0,则-x<0,
从而f(-x)=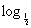 (x+1)=f(x),
(x+1)=f(x),
∴x>0时,f(x)=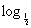 (x+1).
(x+1).
∴函数f(x)的解析式为f(x)=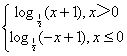 .
.
(Ⅱ)设x1, x2是任意两个值,且x1<x2≤0,
则-x1>-x2≥0,∴1-x1>1-x2.
∵f(x2)-f(x1)
=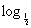 (-x2+1)-
(-x2+1)-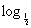 (-x1+1)
(-x1+1)
=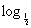
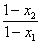 >
>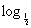 1=0,∴f(x2)>f(x1),
1=0,∴f(x2)>f(x1),
∴f(x)=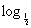 (-x+1)在(-∞, 0]上为增函数. 又f(x)是定义在R上的偶函数,
(-x+1)在(-∞, 0]上为增函数. 又f(x)是定义在R上的偶函数,
∴f(x)在(0, +∞)上为减函数.
∵f(a-1)<-1=f(1),∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞, 0)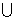 (2, +∞).
(2, +∞).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
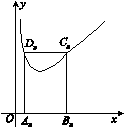
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+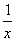 (x>0)的图象上.若点Bn的坐标为(n,0)(n≥2,n∈N*),记矩形AnBnCnDn的周长为an,则a2+a3+…+a10=( )
(x>0)的图象上.若点Bn的坐标为(n,0)(n≥2,n∈N*),记矩形AnBnCnDn的周长为an,则a2+a3+…+a10=( )
A.208 B.216
C.212 D.220
查看答案和解析>>
科目:高中数学 来源: 题型:
设某产品2013年12月底价格为a元(a>0),在2014年的前6个月,价格平均每月比上个月上涨10%,后6个月,价格平均每月比上个月下降10%,经过这12个月,2014年12月底该产品的价格为b元,则a,b的大小关系是 ( )
A.a>b B.a<b C.a=b D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
函数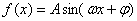 (其中A>0,
(其中A>0,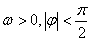 )的图像如图所示,为了得到
)的图像如图所示,为了得到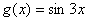 的图像,则只要将
的图像,则只要将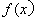 的图像( )
的图像( )
A.向右平移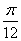 个单位长度
个单位长度
B.向右平移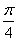 个单位长度
个单位长度
C.向左平移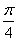 个单位长度
个单位长度
D. 向左平移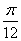 个单位长度
个单位长度 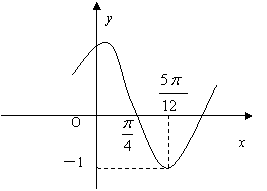
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com