
科目: 来源:江西省高考真题 题型:解答题
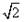 ,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG。
,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG。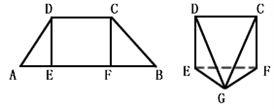
查看答案和解析>>
科目: 来源:广东省月考题 题型:解答题
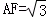 .
.
查看答案和解析>>
科目: 来源:山东省月考题 题型:单选题
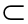 β,则α⊥β;
β,则α⊥β;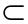 α,n
α,n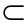 α,m∥β,n∥β,则α∥β;
α,m∥β,n∥β,则α∥β; α,n
α,n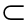 α,m、n是异面直线,那么n与α相交;
α,m、n是异面直线,那么n与α相交;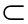 α,n
α,n β,则n∥ α且n∥ β.
β,则n∥ α且n∥ β.查看答案和解析>>
科目: 来源:0113 期中题 题型:解答题
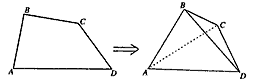
查看答案和解析>>
科目: 来源:0112 月考题 题型:填空题
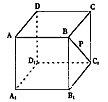
查看答案和解析>>
科目: 来源:0103 模拟题 题型:解答题

查看答案和解析>>
科目: 来源:海南省高考真题 题型:解答题
 。等边三角形ADB以AB为轴转动,
。等边三角形ADB以AB为轴转动,
查看答案和解析>>
科目: 来源:期末题 题型:单选题
[ ]
 ,则b∥α
,则b∥α ,则b⊥α
,则b⊥α查看答案和解析>>
科目: 来源:山东省高考真题 题型:解答题
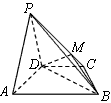
 。
。
查看答案和解析>>
科目: 来源:山东省月考题 题型:解答题
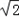 ,CD=1
,CD=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com