12．某商场为了了解顾客的购物信息，随机的在商场收集了100位顾客购物的相关数据，整理如下：

一次购物款（单位：元）	[0，50）	[50，100）	[100，150）	[150，200）	[200，+∞）
顾客人数	m	20	30	n	10

统计结果显示100位顾客中购物款不低于100元的顾客共60位，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．
（Ⅰ）试确定m，n的值，并据上述数据估计该商场每日应准备纪念品的数量；
（Ⅱ）若商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款   小于200元的按购物款的百分比返利，具体见下表：

一次购物款（单位：元）	[0，50）	[50，100）	[100，150）	[150，200）
返利百分比	0	6%	8%	10%

若用各组购物款的中位数估计该组的购物款，请据上述数据估计该商场日均让利多少元？

11．某校有行政人员、教学人员和教辅人员共200人，其中教学人员与教辅人员人数的比为10：1，行政人员有24人，现采取分层抽样的方法抽取容量为50的样本，那么教学人员应抽取的人数为（　　）

A．

30

B．

40

C．

20

D．

36

10．设$a={log_2}π，b={log_{\frac{1}{2}}}π，c=\frac{1}{π^2}$则（　　）

A．

a＞b＞c

B．

b＞a＞c

C．

a＞c＞b

D．

c＞b＞a

9．已知函数f（x）的反函数为g（x）=1+2x，则f（1）=（　　）

A．

0

B．

1

C．

2

D．

4

8．己知向量$\overrightarrow{a}$，$\overrightarrow{b}$，|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=1，且$\overrightarrow{a}$，$\overrightarrow{b}$满足关系：|k$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$+k$\overrightarrow{b}$|，k＞0，设$\overrightarrow{a}$•$\overrightarrow{b}$=f（k）
（Ⅰ）求f（k）的解析式；
（Ⅱ）$\overrightarrow a$能否和$\overrightarrow b$垂直？$\overrightarrow a$能否和$\overrightarrow b$平行？若不能，则说明理由；若能，则求出k值．

7．在平面直角坐标系xoy中，A、B、C是圆x²+y²=1上相异三点，若存在正实数λ，μ，使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$，则λ²+（μ-3）²的取值范围是（　　）

A．

[0，+∞）

B．

（2，+∞）

C．

[2，+∞）

D．

（8，+∞）

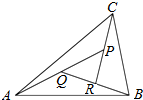6．如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}$=$\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点恰为P，则$\overrightarrow{AP}$等于（　　）

A．

$\frac{1}{2}（\overrightarrow a+\overrightarrow b）$

B．

$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$

C．

$\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$

D．

$\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$

5．已知曲线C的极坐标方程是ρ=2cosθ，直线l的参数方程是$\left\{\begin{array}{l}x=-\frac{2}{3}t+2\\ y=\frac{2}{3}t-5\end{array}\right.$（t为参数）．
（1）将曲线C的极坐标方程化为直角坐标方程；
（2）设直线l与y轴的交点是M，N是曲线C上一动点，求MN的最小值．

4．设S_n=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n×（n+1）}$，求出S₁，S₂，S₃，S₄的值，归纳并猜想出结果．并证明所猜想出结果的正确性．

3．根据给出的数塔猜测123456×9+2等于（　　）

A．

111111

B．

1111111

C．

1111112

D．

1111110