
科目: 来源:2017届重庆市高三文上定时训练数学试卷(解析版) 题型:解答题
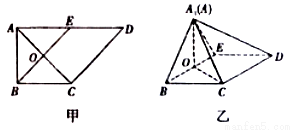
如图,甲,在直角梯形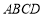 中,
中,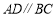 ,
,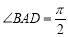 ,
,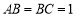 ,
,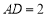 ,
, 是
是 的中点,
的中点, 是
是 与
与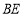 的交点.将
的交点.将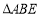 沿
沿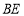 折起到
折起到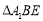 的位置,如图乙.
的位置,如图乙.
(1)证明: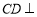 平面
平面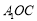 ;
;
(2)若平面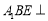 平面
平面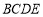 ,求
,求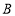 到平面
到平面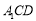 的距离.
的距离.
查看答案和解析>>
科目: 来源:2017届重庆市高三文上定时训练数学试卷(解析版) 题型:解答题
“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了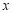 人,按年龄分成5组(第一组:
人,按年龄分成5组(第一组: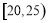 ,第二组
,第二组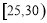 ,第三组:
,第三组: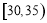 ,第四组:
,第四组: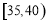 ,第五组:
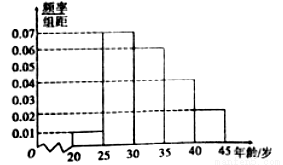
,第五组: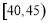 ),得到如图所示的频率分布直方图,已知第一组有6人.
),得到如图所示的频率分布直方图,已知第一组有6人.
(1)求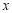 ;
;
(2)求抽取的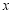 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1-5组,从这5个按年龄分的组合5个按职业分的组中每组各选派1人参加知识竞赛代表相应组的成绩,年龄组中1-5组的成绩分别为93,96,97,94,90,职业组中1-5组的成绩分别为93,98,94,95,90.
(i)分别求5个年龄组和5个职业组成绩的平均数和方差;
(ii)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度,并谈谈你的感想.
查看答案和解析>>
科目: 来源:2017届重庆市高三文上定时训练数学试卷(解析版) 题型:解答题
已知椭圆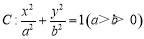 的左、右焦点分别为
的左、右焦点分别为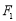 ,
,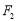 ,椭圆上一点
,椭圆上一点 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于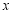 轴.
轴.
(1)求椭圆 的方程;
的方程;
(2)与抛物线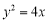 相切于第一象限的直线
相切于第一象限的直线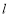 ,与椭圆
,与椭圆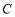 交于
交于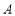 ,
,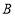 两点,与
两点,与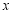 轴交于点
轴交于点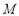 ,线段
,线段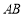 的垂直平分线与
的垂直平分线与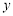 轴交于点
轴交于点 ,求直线
,求直线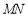 斜率的最小值.
斜率的最小值.
查看答案和解析>>
科目: 来源:2017届重庆市高三文上定时训练数学试卷(解析版) 题型:解答题
已知函数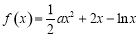 .
.
(1)若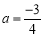 ,判断函数
,判断函数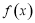 的单调性;
的单调性;
(2)若函数 在定义域内单调递减,求实数
在定义域内单调递减,求实数 的取值范围;
的取值范围;
(3)当 时,关于
时,关于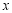 的方程
的方程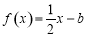 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数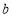 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2017届重庆市高三文上定时训练数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,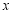 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线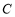 的极坐标方程为
的极坐标方程为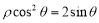 ,它在点
,它在点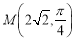 处的切线为直线
处的切线为直线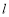 .
.
(1)求直线 的直角坐标方程;
的直角坐标方程;
(2)已知点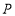 为椭圆
为椭圆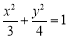 上一点,求点
上一点,求点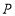 到直线
到直线 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目: 来源:2016-2017学年贵州贵阳六中高一上期中数学试卷(解析版) 题型:选择题
已知集合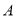 到
到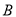 的映射
的映射 ,若
,若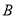 中的一个元素为7,则对应的
中的一个元素为7,则对应的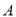 中原像为( )
中原像为( )
A.22 B.17
C.7 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com