
科目: 来源: 题型:
【题目】已知函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,
, ![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.在下列三个函数中:(1)
为“理想函数”.在下列三个函数中:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .“理想函数”有__________.(只填序号)
.“理想函数”有__________.(只填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
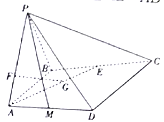
(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设 ![]() 表示学生注意力指标,该小组发现
表示学生注意力指标,该小组发现 ![]() 随时间
随时间 ![]() (分钟)的变化规律(
(分钟)的变化规律(![]() 越大,表明学生的注意力越集中)如下:
越大,表明学生的注意力越集中)如下: 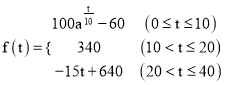 (
(![]() ,且
,且 ![]() )
)
若上课后第 ![]() 分钟时的注意力指标为
分钟时的注意力指标为 ![]() ,回答下列问题:
,回答下列问题:
(1)求 ![]() 的值;
的值;
(2)上课后第 ![]() 分钟时和下课前
分钟时和下课前 ![]() 分钟时比较,哪个时间注意力更集中?并请说明理由.
分钟时比较,哪个时间注意力更集中?并请说明理由.
(3)在一节课中,学生的注意力指标至少达到 ![]() 的时间能保持多长?
的时间能保持多长?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命题p:A∩B≠;命题q:AC.
(1)若命题p为假命题,求实数a的取值范围;
(2)若命题p∧q为真命题,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都乘以同一个非零常数![]() 后,标准差也变为原来的
后,标准差也变为原来的![]() 倍;
倍;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时, ![]() 平均减少5个单位;
平均减少5个单位;
③线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
④在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() ,若
,若![]() 位于区域
位于区域![]() 的概率为0.4,则
的概率为0.4,则![]() 位于区域
位于区域![]() 内的概率为0.6
内的概率为0.6
⑤利用统计量![]() 来判断“两个事件
来判断“两个事件![]() 的关系”时,算出的
的关系”时,算出的![]() 值越大,判断“
值越大,判断“![]() 与
与![]() 有关”的把握就越大
有关”的把握就越大
其中正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
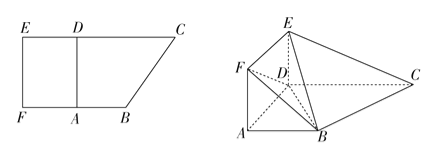
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com